由题意得:三阶幻方的性质(2)构成三阶幻方的九个数,每个数同时乘同一个数或除以同一个不为0的数,所得到的九个数仍能构成三阶幻方.故答案为:构成三阶幻方的九个数,每个数同时乘同一个数或除以同一个不为0的数,所得到的九个数仍能构成三阶幻方.
先将三阶幻方的九个数1,2,3,4,5,6,7,8,9,每个数都乘2,得2,4,6,8,10,12,14,16,18,
根据三阶幻方性质②,2,4,6,8,10,12,14,16,18能构成三阶幻方.
再将2,4,6,8,10,12,14,16,18,每个数都加4得6,8,10,12,14,16,18,20,22,
根据三阶幻方性质①,6,8,10,12,14,16,18,20,22能构成三阶幻方.
所以,6,8,10,12,14,16,18,20,22这九个数能构成三阶幻方,
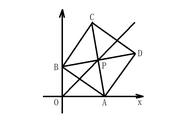
如图⑧,

【点评】本题主要考查数字的变化类,理解题意类比等式的性质是解题的关键.

幻方之美在于其内在的数学原理,在于其外在的完美形态,更在于它无穷无尽的变幻。每个幻方以整齐划一、均衡对称、和谐统一的特性,迸发出耀人的数学之美的光辉。如今,幻方仍然是组合数学的研究课题之一,经过一代代数学家与数学爱好者的共同努力,幻方与它的变体所蕴含的各种神奇的科学性质正逐步得到揭示。在种类上,更加可以细分为完全幻方、乘幻方、多阶幻方、高次幻方,以及反幻方等。当前,幻方已在组合分析、实验设计、图论、数论、群、对策论、纺织、工艺美术、程序设计、人工智能等领域得到广泛应用。可以说,来自远古的幻方,将带领人类走向更高智能的未来。