定时更新最干货的初中数学压轴题型讲解。
如需要本堂内容的word电子版本,请私信与我
想了解更多精彩内容,快来关注初中数学压轴姜老师
青岛中考数学压轴填空题都是线段的求解,线段求解在全国里面非常的常见,这也是考察学生对于几何综合理解的能力。大家可以学习对比,这也是综合几何处理最精彩的地方。

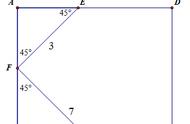
1.(2020•青岛)如图,在正方形ABCD中,对角线AC与BD交于点O,点E在CD的延长线上,连接AE,点F是AE的中点,连接OF交AD于点G.若DE=2,OF=3,则点A到DF的距离为4√5/5.

【分析】
解法一:根据正方形的性质得到AO=DO,∠ADC=90°,求得∠ADE=90°,根据直角三角形的性质得到DF=AF=EF=1/2AE,根据三角形中位线定理得到FG=1/2DE=1,求得AD=CD=4,过A作AH⊥DF于H,根据相似三角形的性质和勾股定理即可得到结论.
解法二:同理得FG的长,利用勾股定理计算DF的长,最后根据△ADF的面积列等式可得AH的长.
【解答】
解:解法一:∵在正方形ABCD中,对角线AC与BD交于点O,

∴AO=DO,∠ADC=90°,
∴∠ADE=90°,
∵点F是AE的中点,
∴DF=AF=EF=1/2AE,
∴OF垂直平分AD,
∴AG=DG,
∴FG=1/2DE=1,
∵OF=3,
∴OG=2,
∵AO=CO,
∴CD=2OG=4,
∴AD=CD=4,
∴AE=√AD² √DE²=√4² √2²=2√5.
过A作AH⊥DF于H,
∴∠H=∠ADE=90°,
∵AF=DF,
∴∠ADF=∠DAE,
∴△ADH∽△EAD,
∴AH/DE=AD/AE,
∴AH/2=4/(2√5),
∴AH=4√5/5,
即点A到DF的距离为4√5/5
,
解法二:在正方形ABCD中,对角线AC与BD交于点O,
∴AO=DO,∠ADC=90°,
∴∠ADE=90°,
∵点F是AE的中点,
∴DF=AF=EF=1/2AE,
∴OF垂直平分AD,
∴AG=DG,
∴FG=1/2DE=1,
∵OF=3,
∴OG=2,
∵AO=CO,
∴CD=2OG=4,
∴AD=CD=4,
∴DG=2,
∴DF=√DG² √FG²=√(4 1)=√5,
过A作AH⊥DF于H,
∴∠H=∠ADE=90°,
∴S△ADF=1/2DF•AH=1/2AD•FG,
∴AH=4√5/5,
故答案为:4√5/5.
【点评】
本题考查了正方形的性质,相似三角形的判定和性质,线段垂直平分线的性质,三角形中位线定理,勾股定理,直角三角形的性质,正确的识别图形是解题的关键.