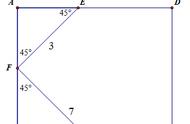
2.(2019•青岛)如图,在正方形纸片ABCD中,E是CD的中点,将正方形纸片折叠,点B落在线段AE上的点G处,折痕为AF.若AD=4cm,则CF的长为 (6﹣2√5) cm.

【分析】
设BF=x,则FG=x,CF=4﹣x,在Rt△GEF中,利用勾股定理可得EF²=(2√5﹣4)² x²,在Rt△FCE中,利用勾股定理可得EF²=(4﹣x)² 2²,从而得到关于x方程,求解x,最后用4﹣x即可.
【解答】
解:设BF=x,则FG=x,CF=4﹣x.
在Rt△ADE中,利用勾股定理可得AE=2√5.
根据折叠的性质可知AG=AB=4,所以GE=2√5﹣4.
在Rt△GEF中,利用勾股定理可得EF²=(2√5﹣4)² x²,
在Rt△FCE中,利用勾股定理可得EF²=(4﹣x)² 2²,
所以(2√5﹣4)² x²=(4﹣x)² 2²,
解得x=2√5﹣2.
则FC=4﹣x=6﹣2√5.
故答案为6﹣2√5.
【点评】
本题主要考查了折叠的性质、勾股定理.折叠问题主要是抓住折叠的不变量,在直角三角形中利用勾股定理求解是解题的关键.

3.(2018•青岛)如图,已知正方形ABCD的边长为5,点E、F分别在AD、DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为√34/2.

【分析】
根据正方形的四条边都相等可得AB=AD,每一个角都是直角可得∠BAE=∠D=90°,然后利用“边角边”证明△ABE≌△DAF得∠ABE=∠DAF,进一步得∠AGE=∠BGF=90°,从而知GH=1/2BF,利用勾股定理求出BF的长即可得出答案.
【解答】
解:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在△ABE和△DAF中,
∵AB=AD
∠BAE=∠D
AE=DF
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∵∠ABE ∠BEA=90°,
∴∠DAF ∠BEA=90°,
∴∠AGE=∠BGF=90°,
∵点H为BF的中点,
∴GH=1/2BF,
∵BC=5、CF=CD﹣DF=5﹣2=3,
∴BF=√BC² √CF²=√34,
∴GH=1/2BF=√34/2,
故答案为:√34/2.
【点评】
本题考查了正方形的性质,全等三角形的判定与性质,直角三角形两锐角互余等知识,掌握三角形全等的判定方法与正方形的性质是解题的关键.