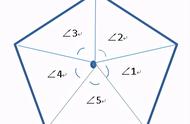
然而,可以想到单元格的其它可能性。即便是六边形也有无数种,但是蜜蜂选择了内角都为120度的六边形。
对这些可替代的形状进行分类,对数学家来说是一项艰巨的任务。
具有相等边和120度角的正六边形的周长比相同区域的任何其它六边形图形的周长相对少一些。此外,边多于六边形的多边形(例如正八边形)效果更好,边数少的多边形(例如正方形)效果更差。
1943年,匈牙利数学家证明了蜂窝猜想。在平面填充模式中,每个单元的平均边数最多为6个。而且,当边数大于六时,产生的优点比边数小于六时的缺点还少,在这种条件下,包围和分隔无限多个相等面积区域的最小周长方法是蜂窝的规则六边形网格。
如果允许单元格具有弯曲的侧面怎么办?数学家考虑了这个问题,并预测最佳答案仍然是规则六边形的网格。

蜂窝猜想可以用于生活上,例如超市最经济的包装方式是一对相同体积的双气泡。在《美国数学学会的五月交易》中,数学家概述了证明六角形蜂窝猜想及其变体的进展。
对于弯曲的六边形侧面,复杂之处在于,一个单元格向外突出的一侧必须向其直接相邻的一侧突出。
海尔斯证明了凸出的优点少于凸出的缺点。如果各种多边形的侧面都弯曲了,在同等条件下,六角形的单元格表现得更好。就是瘸子当中也有将军。
因此,直角多边形比弯曲多边形更好,而正六边形确实是所有多边形中最好的。

但是,除了垂直的六边形网格之外,蜂窝还有更多其它功能。它实际上由两层背靠背放置的单元组成。单元格本身与水平方向成大约13度的角度向上倾斜,刚好足以防止储存的蜂蜜滴落。
每个单元格的底部不是平坦的,而是以三个四边形菱形面板结尾。两层的单元是偏移的,因此一侧的腔室的中心是另一侧的三个相邻单元的角。这样可以使蜂窝各层像安装在一起的两个鸡蛋纸箱的底部那样互锁。然而,在蜂窝中,一层材料用作两个单元的底部。在横截面中,两层之间的界面具有锯齿形结构。

蜂窝单元底部的每个菱形或菱形面的角度分别为109.5和70.5。18世纪,数学家证明了这些特殊的角度可为三菱形配置提供最大的体积。
对数学家来说,许多问题仍然悬而未决。例如,在二维中,单元格的最小面积和最小周长问题已经解决。在三维上,大小相同的单元的最小空间填充结构具有最小表面积的问题仍未解决。
这些问题不仅涉及数学,而且涉及对流体,气泡,泡沫,晶体以及从细胞组合到植物组织的各种生物结构的特征。
细胞和组织,壳和骨骼,叶和花是物质的大多部分,并且服从物理定律,它们的粒子已经被移动,模制和整合。问题首先是数学问题,本质上是物理问题。
蜜蜂的蜂巢整齐地适合自然界中数学上最佳形式的地图集。