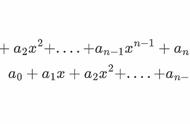来呀,拿出计算器动手试试
a | b | x | f(x)=x^2-2 | b-a |
1 | 2 | 1.5 | 0.25 | 1 |
1 | 1.5 | 1.25 | -0.4375 | 0.5 |
1.25 | 1.5 | 1.375 | -0.109375 | 0.25 |
1.375 | 1.5 | 1.4375 | 0.06640625 | 0.125 |
1.375 | 1.4375 | 1.40625 | -0.022460938 | 0.0625 |
1.40625 | 1.4375 | 1.421875 | 0.021728516 | 0.03125 |
1.40625 | 1.421875 | 1.4140625 | -0.000427246 | 0.015625 |
1.4140625 | 1.421875 | 1.41796875 | 0.010635376 | 0.0078125 |
1.4140625 | 1.41796875 | 1.416015625 | 0.00510025 | 0.00390625 |
1.4140625 | 1.416015625 | 1.415039063 | 0.002335548 | 0.001953125 |
1.4140625 | 1.415039063 | 1.414550781 | 0.000953913 | 0.000976563 |
我们发现,这个虽然很高级,但是精确度还不如竖式计算,精度设置为0.001需要10步,其准确值只有3位小数。
二分法的优点是容易理解,数学上不难,在预设误差条件下还是符合要求的。缺点嘛……不够精确,速度也不快。
第三种解法。牛顿迭代法
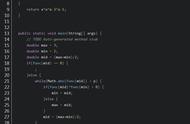
这个解法是这样的,先猜一个数x0,随便猜,然后代入公式

逐个计算。
拿出计算器,先动手试试比较有感觉哈。
n | x |
0 | 4 |
1 | 2.25 |
2 | 1.569444444 |
3 | 1.421890364 |
4 | 1.414234286 |
5 | 1.414213563 |
6 | 1.414213562 |
只要算6次就好了,因为再算下去,结果也是一样,已经不会变了,计算器的精度用尽了。
牛顿迭代的方法优点是快,真快。我猜4已经很变态了,求2的平方根居然猜4,但速度还是超级快。缺点嘛……看不懂,真的看不懂。(呵呵)
那个迭代公式是何方神圣?我把数学过程一写您就明白了。对证明没兴趣的读者可以跳过。

当当当,公式闪亮出场!(不过,我估计您还是不懂)
但凡不懂,就先画个图,说不定就懂了。
求2的平方根,其实就是求