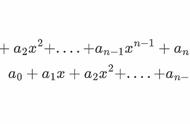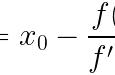看代码的过程中遇到了高斯-牛顿法,感慨于自己作为调包侠,对各种最优化方法知之甚少,于是学习了一下这个算法。费曼技巧推崇以教促学,遂在此写一个简单的教程,希望整理思路以备复习的同时,也能帮助到和我一样的初学者。
本文所涉算法的研究目标是寻找多元二阶可微函数的极小值点,即:

本文首先介绍牛顿法(也称作 Newton-Raphson 方法),然后介绍高斯-牛顿法。
牛顿法
牛顿法的推导基于二阶可微函数的泰勒展开,以一维函数为例:

(2) 式是对f(x)在xn处的二阶近似。如下图所示:

蓝色曲线代表原函数f(x),绿色圆点代表当前点xn,橘黄色的抛物线就是原函数在xn附近的泰勒展开。不难发现,在xn附近,抛物线和原函数曲线基本重合。也就是说,可以用抛物线方程代替原函数方程,而抛物线导函数的零点即为xn 1: