数学作为科学研究的工具,在化学上有十分广泛的应用,今举例说明如下:
一、用排列组合解化学题:
例1.有铝、硝酸铜 、硫酸、苛性钾四种物质,写出它们两两间在一定条件下可以发生反应的化学方程式。
解:按组合公式:C mn =m!/n!﹙m-n﹚!
可知,四种物质的两两组合,总组合数为:
C42=4!/2!﹙4-2﹚!=6
即最多可有六种组合。有关反应为:
1. 铝与硝酸铜溶液
2Al+3Cu(NO3)2=2Al(NO3)3+Cu
2. 铝与硫酸溶液
2Al+3H2SO4=2Al2(SO4)3+3H2↑
3. 铝与苛性钾溶液
2Al+2KOH+2H2O=2KAlO2+3H2↑
⒋ 硝酸铜固体与浓H2SO4
Cu(NO3)2+H2SO4(浓)=CuSO4+2HNO3
⒌ 硫酸和苛性钾溶液
H2SO4+KOH=K2SO4+2H2O
例2. 由1H、2H、16O、17O、18O形成的水分子有( )
(A)5种(B)6种(C)8种(D)9种
解:由于水是由氢、氧两种元素组成的,一个水分子由2个氢原子和1个氧原子构成。
所以,当水分子中只含1H或2H时,只有:
C21C31=2!÷1!×3!÷1!﹙3-1﹚!=2×3=6
当水分子中 1H、 2H均含有时,又有:
C21C31=2!÷2!×3!÷ 1!﹙3-1﹚1!=3
所以,共有6 3=9种水分子,即
1H216O、1H217O、1H218O、
2H216O、 2H217O、2H218O、
1H2H16O、 1H2H17O、1H2H18O
答案为(D)。
运用计算方法进行有关组合题的解答,给我们提供了方便 ,它可以使我们明确地知道其最多组合方式,即上限。然后,再在其内根据实际情况进行有效的组合,尽管有些组合是不合理的,但毕竟可以减小盲目性,增加有效性和准确性。
二、用数列求和法解化学题
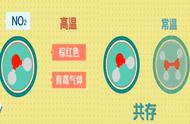
例1.把盛有16毫升NO2气体的试管倒置于水中,问还需向试管中通入多少升氧气,才能使水充满?
解:由于二氧化氮溶于水发生反应:
3NO2 +H2O=2HNO3+NO
其中NO2有1/3转变为NO;通入O2后又发生反应;2NO+O2=2NO2,在水中,生成的NO2又有1/3转变为NO。如此下去,只有当通入足量的O2,使16毫升NO2全部变成HNO3时,才能充满试管。整个过程中量的关系为:
16×1/3+16×1/3×1/3+16×1/3×1/3×1/3
……+16×1/3×1/3……×1/3n个
即:
16×1/3+16×1/3×1/3+16×1/3×﹙1/3﹚2
……+16×1/3×﹙1/3﹚n
这实质上是一个无穷递减等比数列的求和问题,运用无穷递减等比数列的求和公式:
S∞=a1/(1-q)﹙a1为首项,︱q︱<1为公比﹚
此题就很容易求解。
∵a1=16×1/3=16/3
∴S=16/3÷﹙1-1/3﹚=8毫升
由2NO+O2=2NO2知:
所需O2的体积为:8×1/2=4毫升
运用此法能够很容易地解答有关氮的氧化物溶于水的计算。对于类似的须经过多步循环反应才能得计算结果的习题的解答,运用此法也很简便。
例2.已知20℃时CuSO4的溶解度为20克,今将5克无水硫酸铜投入100克20℃CuSO4的饱和溶液中,求能析出几克胆矾晶体?
解:由于无水CuSO4放入饱和CuSO4溶液中,析出胆矾时要带出结晶水,且带出结晶水后,又要析出胆矾,如此往复,直至达到溶解结晶平衡。因此,这也是一个无穷递减等比数列的求和问题。
5克无水CuSO4放入饱和溶液中,第一次带出结晶水量为:
5×5H2O÷CuSO4 =5×90÷160(克)
无水物CuSO4的量为:5×90÷160×20÷100
∵a1=5
q=90÷160×20÷100=9÷80
S=5÷(1-9÷80)=5.63(克)
∴析出的胆矾的量为:5.63×250÷160=8.8(克)
三、用函数关系解化学题
例:今有乙烯和H2的混合气体,设乙烯的摩尔百分数为x%,取1升混和气体,使用催化剂,使之加成完成时,气体体积变为y升,(假定气体体积均在同温同压下测定的),试写出:
(1)当乙烯比H2多时,y和x的函数关系式 y=ƒ(x)
(2)当乙烯比H2少时,y和x的函数关系式y=ƒ(x)
解:由题意知:乙烯为x%,则为H2为(1-x%),
⑴ 当乙烯比H2多时,乙烯过量,以H2为准进行计算
C2H4 + H2 ---→C2H6
1..............1.............1
1-x% 1-x% 1-x%
反应后余下乙烯x%-(1-x%),反应生成的乙烷(1-x%)
反应后的气体为余下的乙烯和反应生成的乙烷之和。其量为:
y=x%-(1-x%)+(1-x%)=x%
⑵ 当乙烯的量比H2少时,乙烯完全反应后生成的乙烷为x%,剩余H2量为:(1-x%)-x%,
反应后的气体为余下的H2和反应生成的乙烷之和。其量为:
y=(1-x%)-x%+x%=1-x%
总之,由上述几例的解答可见,用特殊数学方法解化学习题是行之有效的。它不仅使一些复杂的问题的解答过程变得简捷,而且使解答的结果也更准确。同学们在学习中应注意充分运用数学这一工具解题,以大大的提高解题的能力和效率。