定理的证明

定理推广

费马点结论
以下内容可以不看,因为本人第一次头条发文章,数学类文章,公式经常被系统识别为图片,实在难以编辑,故把自己word里复制在下面,跟上文完全相同----------------------------------------.
费马点定理的证明与补充
1.三角形三个内角均小于120°的情况:
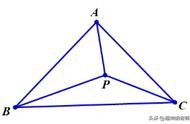
·费马点定理:如果在△ABC内角均小于120°,P为平面内任意一点,若点O对于三边的张角都是120°,则≤(仅当O、P重合时取等号)
证明:过A、B、C分别作OA、OB、OC的垂线,设交于、、,如图所示,则O、B、C、四点共圆,由∠BOC=120°,则∠.
同理∠,故△为正三角形.
设其边长为,则
(因为斜线段大于垂线段)
∴≤.
2.三角形某内角≥120°的情况:
推论:若△中∠≥120°,为平面内任意一点,则≤(只有当、重合时取等于号).
证明:(1)当∠120°时,在△ABC外做∠,连接、,如右图所示,由费马点定理可得
即.
(2)当∠>120°时,在∠内做∠,交于,连接,如右图所示,由(1)有结论:
又,
两不等式左右 分别相加得:
.
综上所述:若△中∠≥120°,则点为费马点,若内角都小于120°,则三角形内部与三边张角均为120°的点为费马点.