幂函数是学习对数函数的基础,学习幂函数,掌握幂函数的概念,常见幂函数的图像及变化特征,会用幂函数的基本性质解决相关问题。
一、幂函数的定义
一般地,形如 y=xα(α为常数)的函数,即底数是自变量、指数是常数的函数称为幂函数.
知识点解析
1.幂的指数是一个常数,它可以取任意实数;
2.幂值前面的系数是1,否则不是幂函数;
3.幂函数的定义域是使xα有意义的所有x的集合,因α的不同,定义域也不同.
二、幂函数的图象和性质
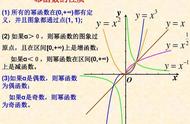
1.常见的五种幂函数的图象
可以发现任一幂函数在第一象限内必有图象,在第四象限内无图象.

2.幂函数的性质

知识点解析
幂函数y=xα的上述性质可归纳如下:
(1)当α>0时,图象都通过点(0,0),(1,1);在第一象限内,函数单调递增.
(2)当α<0时,图象都通过点(1,1);在第一象限内,函数单调递减,图象向上与y轴无限接近,向右与x轴无限接近.
幂函数的概念
判断一个函数是否为幂函数的依据是该函数是否为y=xα(α为常数)的形式,即:(1)系数为1;(2)指数为常数;(3)后面不加任何项.反之,若一个函数为幂函数,则该函数必具有这种形式.
幂函数的图象
(1)本题也可采用特殊值法,如取x=2,结合图象可知2a>2b>2c,又函数y=2x在R上是增函数,于是a>b>c.
(2)对于函数y=xα(α为常数)而言,其图象有以下特点:
①恒过点(1,1).
②当x∈(0,1)时,指数越大,幂函数图象越靠近x轴(简记为“指大图低”);当x∈(1, ∞)时,指数越大,幂函数的图象越远离x轴(简记为“指大图高”).
③由幂函数的图象确定幂指数α与0,1的大小关系,即根据幂函数在第一象限内的图象(类似于y=x-1或y=,y=x3)来判断.
④当α>0时,幂函数在区间(0, ∞)上都是增函数;当α<0时,幂函数在区间(0, ∞)上都是减函数.
利用幂函数的单调性比较大小

1.比较幂大小的三种常用方法

2.利用幂函数单调性比较大小时要注意的问题
比较大小的两个实数必须在同一函数的同一个单调区间内,否则无法比较大小.