一、引言
幂函数是高中数学中的一类重要函数,它在函数理论、数学分析、实际应用等方面都具有重要地位。幂函数的形式简单,性质丰富,是研究函数性质、解决数学问题的有力工具。本文将详细解析幂函数的概念、性质、图像特点以及应用,帮助同学们更好地掌握这一知识点。

二、幂函数的概念
幂函数是指形如y = x^a(a为常数)的函数,其中x是自变量,a是幂指数。幂函数是一种基本的初等函数,其定义域和值域都与幂指数a的取值有关。
三、幂函数的性质
- 定义域和值域:当a为整数时,幂函数的定义域为全体实数;当a为非整数时,幂函数的定义域需要排除使x^a无意义的点。幂函数的值域通常根据a的取值和定义域来确定。
- 单调性:当a > 0时,幂函数在其定义域内是增函数;当a < 0时,幂函数在其定义域内是减函数。这一性质与一次函数和二次函数的单调性类似。
- 奇偶性:当a为整数时,若a为偶数,则幂函数为偶函数;若a为奇数,则幂函数为奇函数。当a为非整数时,幂函数通常既不是奇函数也不是偶函数。
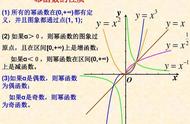
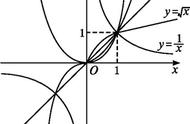
- 过定点:所有幂函数都过点(1,1),即当x=1时,y=1。此外,对于特定的a值,幂函数还可能过其他定点,如y = x^2过点(0,0)。
- 导数性质:幂函数的导数可以通过求导公式得到,即(x^a)' = ax^(a-1)。这一性质在求解与幂函数相关的导数问题时非常有用。
四、幂函数的图像特点
- 形状:幂函数的图像通常是一条经过原点的曲线。当a > 0时,图像在第一象限内上升;当a < 0时,图像在第一象限内下降。随着|a|的增大,图像的弯曲程度逐渐增大。
- 位置:当a为偶数时,图像关于y轴对称;当a为奇数时,图像关于原点对称。对于非整数的a值,图像通常不具有对称性。
- 渐近线:当a < 0时,幂函数的图像在x轴上方有一条水平渐近线y=0;当a > 1时,图像在x轴上方有一条斜渐近线y=x。这些渐近线描述了函数在无穷远处的行为特点。
五、幂函数的应用
- 解决实际问题:在实际生活中,很多问题可以通过建立幂函数模型来解决。例如,在物理学中描述物体的运动规律、在经济学中分析成本收益关系等都可以利用幂函数进行建模和分析。
- 数学分析基础:幂函数作为一类基本的初等函数,在数学分析中扮演着重要角色。通过研究幂函数的性质和行为特点,可以为后续学习更复杂的数学知识和解决更复杂的数学问题打下基础。
- 拓展数学思维:通过学习和研究幂函数及其性质和应用实例,可以拓展学生的数学思维方式和能力水平。学生可以从不同角度思考和解决问题,提高分析问题和解决问题的能力。
六、典型例题分析
本部分将通过具体的例题,详细解析如何利用所学知识判断和分析幂函数的性质和行为特点以及解决相关问题。包括求定义域和值域、判断单调性和奇偶性、绘制图像等不同方面的应用实例。通过分析和解答这些例题,同学们可以加深对幂函数知识点的理解并提升解题能力。
七、总结与展望
通过本文的学习同学们对“幂函数”这一知识点有了更深入的理解。掌握这一知识点不仅有助于提高学生的数学素养和解决问题的能力还为后续的学习和应用奠定了坚实的基础。希望同学们在未来的学习中不断巩固和应用这一知识点探索更多与之相关的有趣性质和应用实例。同时也期待教育工作者和研究者们能够不断完善和拓展这一领域的教学内容和方法为学生提供更加优质的教育资源和指导。通过不断地学习和实践我们相信同学们一定能够熟练掌握这一知识点并在实际生活中加以应用。