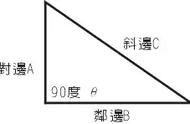
分析与解:显然,A、B、C、D都是动点,直接考虑DO的长与已知矩形ABCD的边长的关系是不可能的.
由于矩形在运动过程中形状不变,所以AB总是等于2,
注意到∠AOB=90°,故AB的中点到O的距离总是等于AB/2=1,
因此,取AB的中点E,连结OE、DE、OD,
则OE=1(直角三角形斜边上的中线等于斜边的一半),
由勾股定理,得DE=√2,
从而DE+EO=√2+1.
由于当D、E、O三点不在同一直线上时,总有DO<DE+OE,
故当D、E、O三点共线时,
OD=OE+DE为最大,等于√2+1.
因此,当矩形运动到点D、AB的中点E和点O三点共线时,
点D到点O的距离最大,为√2+1.
友情提示:对于任意三点A、B、C,总有AB≤BC+CA,当A、B、C三点共线时,等号成立,AB取最大值.求动点到定点距离最大值问题往往就是根据这个原理.
三、利用垂线段最短
例4 以边长为2的正方形的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于A、B两点,则线段AB的最小值是________.
分析与解:根据题意画出如图4,由题意,点A、B都是动点,
由勾股定理,得AB=√(OA2 OB2),
能否进一步转化呢?
考虑已知条件,由四边形CDEF为正方形,得
OC=OD,∠OCA=∠ODB=45°,∠COD=90°,
由∠AOB=90°,得∠COA=∠DOB,
所以△COA≌△DOB,
所以OA=OB,△AOB为等腰直角三角形,
故可将AB进一步转化为AB=√2OA,
问题转化为确定点A的位置,使得OA最小.
由于O是定点,A在定直线CD上,
所以当OA垂直于CD时,垂足就是点A的位置.
因此,作OA⊥CD于A,此时OA=1,
从而AB=√2,故线段AB的最小值为√2.

友情提示:直线上的动点到定点的距离最小值是该定点到该直线的垂线段长.
例5 如图5,正方形ABCD中,AB=1,P是AC上的动点,则PA PB PD的最小值是__________.

分析与解:显然,PB=PD,
所以PA PB PD
=PA 2PD=2(PA/2 PD),
接下来设法将PA/2转化为一条新的线段.作∠CAE=30°,CE交BC于E,作PF⊥AE于F.
则PF=PA/2,于是
PA PB PD =2(PF PD)≥2DF.
所以当DF⊥AE时,PA PB PD=2DF最小.
在RT△ADF中,∠DFA=90°,∠DAF=75°,AD=1,
由sin75°=sin(30° 45°)
=sin30°cos45° cos30°sin45°
=(√2 √3)/4,
所以DF=ADsin75°=(√2 √3)/4.
友情提示:几何中的ax y(a为常数,x,y为图中的动线段)最小值问题的解法,关键在于寻找与ax相等的线段z,将问题转化为z y最小值问题.
四、利用平行距离最小
例6 已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.
问题1:如图6-1,P为AB边上一点,以PD、PC为边做平行四边形PCQD,请问对角线PQ、DC的长能否相等,为什么?

问题2:如图6-2,P为AB边上任意一点,以PD、PC为边做平行四边形PCQD,请问对角线PQ,的长是否存在最小值?如果存在,请求出最小值;如果不存在,请说明理由;
问题3:P为AB边上任意一点,延长PD到E,使DE=PD,以PE、PC为边做平行四边形PCQE,请探究对角线PQ,的长是否也存在最小值?若果存在,请求出最小值;如果不存在,请说明理由;
问题4:如图6-3,P为DC边上任意一点,延长PA到E,使AE=NPA,(N为常数)以PE、PB为边做平行四边形PBQE,请探究对角线PQ的长是否也存在最小值?若果存在,请直接写出最小值;如果不存在,请说明理由.
分析与解:问题1:假设对角线能相等,即PQ=CD,
则四边形PCQD是矩形,
所以∠DPC=90°,
因为AD=1,AB=2,BC=3,
所以DC=√[(3-1)2 22]=2√2,
设PB=x,则AP=2-x,
在Rt△DPC中,PD2+PC2=DC2,
即x2+32+(2-x)2+1=8,
化简得x2-2x+3=0,
因为△=(-2)2-4×1×3=-8<0,
方程无实数根,所以对角线PQ、DC的长不可能相等;
问题2:显然,PQ的长与点P的位置有关,要判断PQ是否存在最小值,关键在于确定点Q在什么线上运动?
过点Q作BC的垂线L,交BC延长线于点H.
则L∥AB.因为AD∥BC,
所以∠ADC=∠DCH,
即∠ADP+∠PDG=∠DCQ+∠QCH,
因为PD∥CQ,所以∠PDC=∠DCQ,
所以∠ADP=∠QCH,又PD=CQ,
所以RT△ADP≌RT△HCQ,
所以AD=HC.
因为AD=1,BC=3,
所以BH=4,
可见,直线L是定直线.由于点P、Q分别在距离为4个单位的两条平行线上运动,
所以当PQ⊥AB时,PQ的长最小,为4;