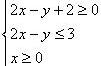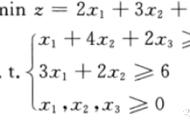论文中常出现的数学规划问题与求解方法 Ⅰ中,提到两个问题:
需要得到从两个未知数优化问题向着多个未知数优化问题的范式流程吗?
这样的范式流程,会是单纯形法吗?
答案显而易见,不是的。
举出这个经典的例子,本意是从中抽离出一种求解思想:确保每一步解的状态变化转移向最优靠近的思想。
实际中,走出教学和科研圈子,论文写作中,只要初步了了解单纯性法的思想、步骤,适用前提,结果表达即可。
我们将思路从新回到原本的问题上,利用单纯性法来求解该工厂月度最优生产规划。首先,需要构建一个规范且简单的模型。
由于目标函数和约束条件内容和形式上的差别,线性规划问题可以有多种表达式。因此,为了讨论和制定统一的算法,在制定单纯形法时,规定使用单纯形法求解的首先,求解线性规划问题需要有一个标准形式,它有下面三个特征:
(1) 标准形式目标函数统一为求极大值或极小值;
(2) 所有约束条件(除非负条件外)都是等式,约束条件右端常数项b全为非负值;
(3) 所有变量的取值全为非负值。
易知,本文最开始探究的工厂问题正是一个标准形式下的线性规划问题。
原本的约束式左边(例如第三个限制式的左边为X1 X2 X3)均是小于或等于右边的约束值(例如第三个限制式的右边为23),那么当右边的约束值减去左边的约束式,会出现一个大于等于零的差值。我们将这个差值设为新的变量,也叫做松弛变量。
假设上面三个约束式的松弛变量为X4,X5,X6。那么可得到以下的式子:
设置目标最大值为Z。Z等于上式中的max。基于工整性原则,调整所有等式的左边均是未知项,等式右边均为常数。将引入新的变量后的式子提炼出系数矩阵,可得其系数矩阵表如下所示:
等式右设每一个等式的基向量表达为BV(Base variable),目标函数值式子记为eq(0),约束式依次记为eq(1)、eq(2),eq(3)。
得如下所示:
以上的三类元素,即可构成一整表,即为单纯形表,如下所示:接下来,需要按照前文提到的“向更优靠近”的原则,对单纯形表进行矩阵转换。
易知,X2的目标函数值系数为-4,大于X1和X3的系数,所以第一步尽量满足X2取值最大。X2在式子0、1、2 , 3中取值最大分别为25、15,15。该未知数取值必须满足所有限制式,故其应该取25和15中较小的那一个,即为15。
给式子eq(2)中的X2取值为15,那么其他约束值中的X2就为零。此刻给X2进行赋值,X2转换为基变量,其他式子中的X2系数转换为零,单纯形法转换结果如下所示:
接下来,继续按照“向更优靠近”的原则处理矩阵。易知此时X3在目标函数中的系数为-1<0,此时保证取X3的最大值。
X3在在限制式eq(1)中最大取20,,限制式eq(2)中最大取值为30,故应该取X3为20。得到的单纯形表变换如此时,目标函数式eq(0)中的式子均大于零,无可优化选项,以上即得最优解。由表可知,目标函数最优值为80,最优解X1=0,X2=5,X3=20。
这与我们在往期文章中求出来的结果是一致的。以下即为往期文章中利用优化软件lingo进行求解的结果
有的读者朋友或许会问,既然lingo求解这么快,这么直接,那么你为什么还要介绍单纯形法,给我带了理解上的巨大苦痛?
其实,在论文中使用单纯形法最大的好处,就是帮助充实文章内容了。多一种研究方法,多几大段的求解过程,论文的整体水平大大提升。
在对线性规划的内容和方法有一定了解后,我们以具体的论文为例,来说说论文中线性规划的表现。
有许多的硕博士论文时以线性规划问题在成本分配中的应用研究为例,利用线性规划问题展开研究的。我们以其中的一个小方向——辅助车间成本分配来展开。
与线性规划解法相对应的,辅助车间成本分析中常用到的方法有交互分配法、直接分配法、代数法。
采用交互分配法,计算繁琐,运算环节多,准确性不够高。直接分配法不考虑各辅助生产车间内部互供量,造成成木归集不准确,直接影响到基本生产成本分配;代数法计算过程相对繁琐,需运用数学软件来进行求解,存在人为定价因素,所求得的解不是最优解。
而线性规划法虽然在模型建立过程中较为困难,但是其可以反映分布交互步骤,逐步修正,并且计算精准,其计算的成本优化精准性最高,优化性最强。
这样的一篇文章,基本内容是模仿方法对比,模型结果对比。整个文章层次井然、条理清晰,其实用性、学术性都是极佳。
有人会问,我在解决辅助车间成本分配,怎么就牵扯到了学术性了?
这地方需要加深的理解是,线性规划问题乃至所有规划问题的提出,本身就是建立在求解现实问题的基础上的。在求方法对比的研究汇总中,一般可分为两大类:
第一类是纯数学模型的理论分析与结果展示,一类是结合实际问题的理论分析与实际目标效益的结果展示。
第一类是普遍性的,广泛的;
第二类是特殊性的,具体的。
两类问题相互佐证,才能真正程度上说明线性规划问题提出的巨大意义。
这种方法对比类的文章是论文中利用线性规划问题中常见的模式,除此之外,还有一种常见的,是利用线性规划模型和其他方法模型进行连接,构造出解决问题的新模型。
例如,在解决运输问题中利用区域划分法划分结果下的线性规划问题进行求解,在物流绩效评价中结合线性规划识别和层次分析法一并做绩效评估。
往后的文章,还会介绍非线性规划的问题。此处先略微提及下:非线性规划是一种求解目标函数或约束条件中有一个或几个非线性函数的最优化问题的方法。非线性规划在实际生活中的应用深度和广度是远远大于线性规划的。
举个简单的例子,下面的模型即为简单的非线性规划
那么我们在论文写作中,还需要学会手动求非线性规划的解法吗?
答案同上,需要的。
学lingo有用吗?
有用的,可以避免自己计算结果出现失误,作为一种查验工具,实在是再好不过了。
但是类似于手撕榴莲的手算过程,也是必要的。字数嘛,深度嘛,要扩充的。
不扩充?是不可能不扩充的,不扩充,这辈子都不可能不扩充的。论文内容和深度都不够,只有无脑扩充才能解决的样子。