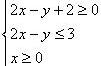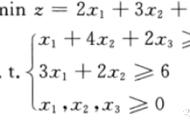求线性目标函数在线性目标条件下的最值问题称为线性规划问题。基本步骤是:
1、确定好线性约束条件,准确画出可行域。
2、对目标函数z=ax by,若b>0,则

取得最大值(或最小值)时,z也取得最大值或最小值;若b<0,则反之。
3、一般地,可行域的边缘点有可能是最值点,有些问题可代入边缘点找最值.
4、注意实际问题的特殊要求。
例、有一批钢管,每根长度都是4000mm,现在要将每根钢管截成长为500mm和600mm的两种毛坯,且这两种毛坯的数量比大于

,问:怎样截最合理?
分析:设每根钢管截成的500mm毛坯为x根,600mm毛坯为y根,则根据已知条件可列出对应的线性约束条件,所谓的最合理应是每根钢管截出的两种毛坯最多。即z=x y取得最大值,但要注意x,y都是正整数,即在可行域内要找到整点。
解:设每根钢管截成的500mm毛坯为x根,600mm毛坯为y根。
则