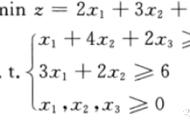这说明该厂的最优生产计划方案是:生产4件产品Ⅰ,2件产品Ⅱ,可得最大利润为14元。
2.解的讨论
在上述例题中,得到的最优解是唯一的,但对一般线性规划问题而言,求解结果还可能出现以下几种情况:无穷多最优解(多重解),无界解(无最优解),无可行解。当求解结果出现后两种情况时,一般说明线性规划问题的数学模型有错误。无界解源于缺乏必要的约束条件,无可行解源于矛盾的约束条件。
从图解法中直观地看到,当线性规划问题的可行域非空时,它是有界或无界凸多边形。若线性规划问题存在最优解,它一定在可行域的某个顶点得到;若在两个顶点同时得到最优解,则它们连线上的任意一点都是最优解,即有无穷多最优解。
3.单纯形法
图解法虽然直观,但当变量数多于3个以上时,它就无能为力了,这时需要使用单纯形法。
单纯形法的基本思路是:根据问题的标准,从可行域中某个可行解(一个顶点)开始,转换到另一个可行解(顶点)。并且使目标函数达到最大值时,问题就得到了最优解。限于篇幅,本书不再介绍单纯形法的详细求解过程。
4.线性规划的适用性
线性规划模型用在原材料单一、生产过程稳定不变、分解型生产类型的组织是十分有效的,例如,石油化工厂等。对于产品结构简单、工艺路线短,或者零件加工组织,有较大的应用价值。需要注意的是,对于机电类组织用线性规划模型只适用于作年度的总生产计划,而不用来做月度计划。这主要与工件在设备上的排序有关,计划期太短,很难安排过来。
一般来说,一个经济管理问题满足以下条件时,才能建立线性规划的模型。
(1)要求解问题的目标函数能用数值指标来反映,且为线性函数。
(2)存在着多种方案。
(3)要求达到的目标是在一定约束条件下实现的,这些约束条件可用线性等式或不等式描述。