模拟退火算法应用方法,模拟退火算法的改进方法

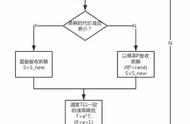
其中a常取值0.5~0.9, 这种退火策略很常用。

1. 经典的模拟退火衰减函数（对数降温）为：

1. 可以选择其它的衰减函数：

衰减函数应选择小的比较合适，可避免过长的马尔可夫链和迭代次数增加。

内循环终止的准则，也称为Metropolis抽样稳定准则，用于决定各温度下产生候选解的个数，该准则包括有：目标函数的平均值是否稳定；连续若干步目标函数值变化较小；按一定的步数抽样。

外循环终止的准则，即决定算法何时结束，主要包括：循环迭代的次数设置；终止温度的阈值设置；检验系统熵值是否稳定；检验算法收敛到最优值连续若干步保持不变。其中终止温度的设置常用的是Kirkpatrick等提出准则：在若干个马尔可夫链中解无任何变化（恶化或优化）就终止算法。迭代次数L的选取与冷却进度表密切相关，一般T衰减小，则 L值就适当大。

模拟退火算法的应用很广泛，可以求解NP完全问题，但其参数难以控制，其主要问题有以下几点：

状态转换很重要，状态的搜索、跳转策略直接影响着算法的性能。可采用附加扰动、随机产生、移位、平滑、边界取值等多种算子作为状态产生函数X(i 1) = G(Xi)。

比如根据具体的问题去分析，状态有没有边界，如果有边界的话，在状态跳转时要用边界限制。状态转换是从当前状态至下一状态，每一次跳动都是随机的，但不是完全随机的，是在一定范围内进行的跳动。那么，两个问题来了，

• 范围怎么确定?
• 范围确定后，状态怎么转换?

退火的跳动幅度是随着温度的下降逐渐降低的，因此，跳动范围须与温度建立关系，随温度下降，跳动范围减少。这个减少可以是线性的，也可以是非线性的。范围确定了，下一次状态的跳转可由高斯随机数生成，通过控制高斯方差就可以控制跳动范围。

状态转换完全随机会怎样？完全随机意味着 状态开始时乱跳，温度降下来后也乱跳，这就就违背了退火算法思想。

温度T的初始值设置是影响模拟退火算法全局搜索性能的重要因素之一。初始温度高，则搜索到全局最优解的可能性大，但因此要花费大量的计算时间；反之，则可节约计算时间，但全局搜索性能可能受到影响。

一般要求初始值T0的值要充分大，即一开始就处于高温状态，且Metropolis的接收率约为1。 在无限高温时，系统立即均匀分布，接受所有提出的变换。实际应用过程中，初始温度一般需要依据实验结果进行若干次调整。

衰减函数用于控制温度的退火速度，一个常用的指数函数为：T(n 1) = K*T(n)，其中K是一个非常接近于1的常数。

T的衰减越小，T到达终点的时间越长，但可使马可夫链长越小，到达准平衡分布的时间越短，

马可夫链长度L是指每一次随机游走过程，要迭代多少次，才能趋于一个准平衡分布，即一个局部收敛解位置。

原则是，在衰减参数T的衰减函数已选定的前提下，L应选得在控制参数的每一取值上都能恢复准平衡。

有很多种终止条件的选择，各种不同的条件对算法的性能和解的质量有很大影响。这里介绍一个常用的终止条件，即上一个最优解与最新的一个最优解的之差小于某个容差，就可停止此次马尔可夫链的迭代。

有效的参数选择判据是：

• 算法的收敛：主要取决于衰减函数和马可夫链的长度及停止准则的选择；
• 算法的实验性能：最终解的质量和CPU的时间。

解：根据题意，我们设计参数为：

Metropolis的步长为0.02

初始温度为100

衰减参数为0.95

马可夫链长度为10000

结束条件为根据上一个最优解与最新的一个最优解的之差小于某个容差。

1) 设计合适的状态产生函数，使其根据搜索进程的需要表现出状态的全空间分散性或局部区域性；

2) 设计高效的退火策略；

3) 避免状态的迂回搜索；

4) 采用并行搜索结构；

5) 为避免陷入局部极小，改进对温度的控制方式；

6) 选择合适的初始状态；

7) 设计合适的算法终止准则。

通过对模拟退火算法的要素的改进或与其它算法相结合可提高模拟退火算法的性能。

1. 提升初温。算法初始化，增加升温或重升温过程，将温度适当提高，以激活各状态的接受概率，可以避免算法在局部极小解处停滞不前。
2. 增加记忆功能。增加存储环节，将当前最好状态记录下来，避免搜索过程由于因根据 Metropolis准则接受当前解时，可能丢掉当前遇到的最优解。
3. 增加补充搜索过程。在退火结束后，把当前最优解设置为初始状态，再次执行模拟退火过程或局部性的搜索。
4. 多次搜索策略。对每一当前状态，采用多次搜索策略，取代标准SA算法的单次比较方式。

混合模拟退火算法，模拟退火与遗传算法相结合。近年来，模拟退火算法与遗传算法的融合在计划调度、机器人研究、软硬划分等方向均有应用。因此，今后要进一步深入研究 SA 与 GA 算法的结合，充分利用双方的优势，使其在相应的科学领域发挥更大的作用。

模拟退火算法可以较高的效率求解很多问题, 应用也非常广泛。

1、最大截问题(Max Cut Problem)

2、0-1背包问题(Zero One Knapsack Problem)

3、图着色问题(Graph Colouring Problem)

4、调度问题(Scheduling Problem)

5、在VLSI设计中的应用

利用模拟退火算法进行VLSI的最优设计，是目前模拟退火算法最成功的应用实例之一。用模拟退火算法几乎可以很好地完成所有优化的VLSI设计工作。如全局布线、布板、布局和逻辑最小化等等。

6、在神经网计算机中的应用

模拟退火算法具有跳出局部最优陷阱的能力。在Boltzmann机中，即使系统落入了局部最优的陷阱，经过一段时间后，它还能再跳出来，再系统最终将往全局最优值的方向收敛。

7、在图像处理中的应用

模拟退火算法可用来进行图像恢复等工作，即把一幅被污染的图像重新恢复成清晰的原图，滤掉其中被畸变的部分。因此它在图像处理方面的应用前景是广阔的。

8、模拟退火算法的其他应用

除了上述应用外，模拟退火算法还用于其它各种组合优化问题，如TSP和Knapsack问题等。大量的模拟实验表明，模拟退火算法在求解这些问题时能产生令人满意的近似最优解，而且所用的时间也不很长。