通常,数组用循环来处理,一般来说,一维数组的数据处理可以使用单重循环或双重循环。如输出数组元素值,从一个数组中挑选最大值或最小值等可以使用单重循环。而对于数组的排序一般使用双重循环,因为单重循环可以挑出一个元素的最大值或最小值,而有n个元素的数组则通过n次挑选便可完成整个数组的排序,所以在单重循环外再嵌套一个循环即可。
对于二维数组的数据处理,通常可以使用双重循环或三重循环,如二维数组元素值的输出,便可以使用双重循环,而矩阵(二维数组)乘法,便可以使用三重循环:
const int maxn=105;
int a[maxn][maxn],b[maxn][maxn];
int ans[maxn][maxn];
int a_n,a_m,b_n,b_m;
void mul(){
for(int i=0; i<a_m; i ){ // i循环数组a的行
for(int j=0; j<b_n; j ){// j循环数组b的列
for(int k=0; k<a_n; k ){ // k循环数组a的列,数组b的行,
ans[i][j] =a[i][k]*b[k][j];
}
}
}
三重循环的另一个经典应用就是Floyd算法求多源最短路径。
Floyd算法又称为插点法,是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
其算法的核心是在顶点 i 和顶点 j 之间,插入顶点k,看是否能够缩短 i 和 j 之间的距离(松驰操作)。
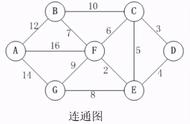
暑假,小哼准备去一些城市旅游。有些城市之间有公路,有些城市之间则没有,如下图。为了节省经费以及方便计划旅程,小哼希望在出发之前知道任意两个城市之前的最短路程。

可以画成如下的简图↓

上图中有4个城市8条公路,公路上的数字表示这条公路的长短。请注意这些公路是单向的。我们现在需要求任意两个城市之间的最短路程,也就是求任意两个点之间的最短路径。这个问题这也被称为“多源最短路径”问题。
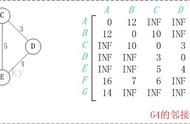
现在需要一个数据结构来存储图的信息,我们可以用一个4*4的矩阵(二维数组e)来存储。比如1号城市到2号城市的路程为2,则设e[1][2]的值为2。2号城市无法到达4号城市,则设置e[2][4]的值为∞。另外此处约定一个城市自己是到自己的也是0,例如e[1][1]为0,具体如下↓

现在回到问题,如何求任意两点之间最短路径呢?
我们来想一想,从a到b,直接相连(到达)不一定是最短的,如果经过第三个点(顶点k),并通过这个顶点k中转即a->k->b,有可能是从顶点a点到顶点b的最短路程。那么这个中转的顶点k是1~n中的哪个点呢?甚至有时候不只通过一个点,而是经过两个点或者更多点中转会更短,即a→k1→k2→b或者a→k1→k2→…→ki→b。
比如上图中从4号城市到3号城市(4→3)的邻接路程e[4][3]原本是12。如果只通过1号城市中转(4→1→3),路程将缩短为11(e[4][1] e[1][3]=5 6=11)。其实1号城市到3号城市也可以通过2号城市中转,使得1号到3号城市的路程缩短为5(e[1][2] e[2][3]=2 3=5)。所以如果同时经过1号和2号两个城市中转的话,从4号城市到3号城市的路程会进一步缩短为10。通过这个的例子,我们发现每个顶点都有可能使得另外两个顶点之间的路程变短。好,下面我们将这个问题一般化。
当任意两点之间不允许经过第三个点时,这些城市之间最短路程就是初始路程,如下↓