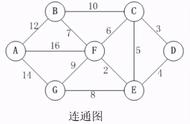
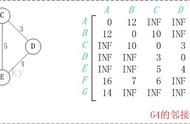
通过上图得知,在相比只允许通过1号顶点进行中转的情况下,这里允许通过1和2号顶点进行中转,使得e[1][3]和e[4][3]的路程变得更短了。
同理,继续在只允许经过1、2和3号顶点进行中转的情况下,求任意两点之间的最短路程。任意两点之间的最短路程更新为:

最后允许通过所有顶点作为中转(在双重循环外再嵌套一个循环),任意两点之间最终的最短路程为:

整个算法过程虽然说起来很麻烦,但是代码实现却非常简单,核心代码就是一个三重循环:

这段代码的基本思想就是:最开始只允许经过1号顶点进行中转,接下来只允许经过1和2号顶点进行中转……允许经过1~n号所有顶点进行中转,求任意两点之间的最短路程。用一句话概括就是:从i号顶点到j号顶点只经过前k号点的最短路程。其实这是一种“动态规划”的思想。
Floyd算法可以求出任意两个点之间最短路径。它的时间复杂度是O(n³),空间复杂度是O(n²)。令人很震撼的是它竟然只有五行代码,实现起来非常容易。
Floyd算法适用于APSP(All Pairs Shortest Paths,多源最短路径),是一种动态规划算法,稠密图效果最佳,边权可正可负。此算法简单有效,由于三重循环结构紧凑,对于稠密图,效率要高于执行V(V为顶点数)次Dijkstra算法,也要高于执行V次SPFA算法。
优点:容易理解,可以算出任意两个节点之间的最短距离,代码编写简单。
缺点:时间复杂度比较高,不适合计算大量数据。
如果需要求出各点之间最短路径所经过的节点,只需增加一个前驱数组即可。如p[i][j],当点p[i][j]经过k点能取得更短路径时,令
p[i][j]=p[k][j]; // 更改j的前驱为k
如点4至点3的最短距离为:10,路线:4 1 2 3,是怎样求出来的呢?程序运行完后,由数组p[i][j]即可得出此路径(参照最后源代码和最后运行结果):
p[4][3]=2
p[4][2]=1
p[4][1]=4 // i=p[i][j]时结束路径搜索
因为是按顺序求出的前驱,所以颠倒一下顺序(使用栈)即可。
Floyd算法由Robert W. Floyd(罗伯特·弗洛伊德)于1962年发表在“Communications of the ACM”上。同年Stephen Warshall(史蒂芬·沃舍尔)也独立发表了这个算法。所以该算法也称为Floyd-Warshall算法。Robert W.Floyd这个牛人是朵奇葩,他原本在芝加哥大学读的文学,但是因为当时美国经济不太景气,找工作比较困难,无奈之下到西屋电气公司当了一名计算机操作员,在IBM650机房值夜班,并由此开始了他的计算机生涯。此外他还和J.W.J. Williams(威廉姆斯)于1964年共同发明了著名的堆排序算法HEAPSORT(堆排序算法)。Robert W.Floyd在1978年获得了图灵奖。
Robert W.Floyd(1936-2001)↓