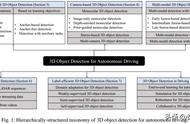
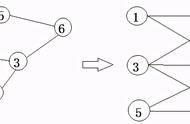
1、最小生成树与最短路径
定义:最小生成树:保证整个拓扑图的所有路径之和最小(连接所有节点),但不能保证任 意两点之间是路径最短,如:各城市天然气管道的架设,如何规划保证使用最少的管 道。P864
最短路径:保证从起点到达目的地的路径最小即可,无需连接所有节点。P867
区别:最小生成树构成后所有的点都被连通,而最短路只要到达目的地走的是最短的路径即可,与所有的点连不连通没有关系。
结论:1、遇到求所有路径之和最小的问题用最小生成树&并查集解决;
2、遇到求两点间最短路径问题的用最短路,即从一个城市到另一个城市最短的路径问题。
2、匈牙利法
算法步骤:
1)对指派问题的系数矩阵进行变换,使每行每列至少有一个元素为“0”.
①让系数矩阵的每行元素去减去该行的最小元素;
②再让系数矩阵的每列元素减去该列的最小元素。
接下来只需要找到0所在位置进行对应的分配即可:
(2)从第一行开始,若该行只有一个零元素,就对这个零元素加括号,对加括号的零元素所在的列画一条线覆盖该列,若该行没有零元素或者有两个以上零元素(已划去的不算在内),则转下一行,依次进行到最后一行。
(3)从第一列开始,若该列只有一个零元素。就对这个零元素加括号(同样不、考虑已划去的零元素)。再对加括号的零元素所在行画一条直线覆盖该列。若该列没有零元素或有两个以上零元素,则转下一列,依次进行到最后一列为止。
(4)重复上述步骤(1)和(2)可能出现3种情况:
①效率矩阵每行都有加括号的零元素,只要对应这些元素令 就找到了最优解。
②加括号的零元素个数少于m,但未被划去的零元素之间存在闭回路,这时顺着闭回路的走向,对每个间隔的零元素加一个括号,然后对所有加括号的零元素所在行(或列)画一条直线,同样得到最优解。
应用:
在实际中经常会遇到这样的问题,某单位需要完成n项任务,恰好有n个人可以承担这些任务。由于每个人的专长不同。同一件工作由不同的人去完成,效率(例如所花的时间或费用)是不同的,于是就会出现应分配哪个人去完成哪项任务,使完成这几项任务的总效率最高(例如总时间最省、总费用最少等).这类问题称为分配问题,又称为指派问题。 [2]
匈牙利法是最优利用生产资源,计算、调整最优分配方案变量的经营分析方法。其目的和衡量标准是在对资源、材料分配中的已知数据作变换处理的基础上,提出所求取的目标对象(被测算的产品资源)的最优分配方案,它们的机会成本最小。即以未被采用的方案所造成的损失来衡量、评价被选择方案的假定成本为零值方式,论证分配方案的最优化程度。其特点是在求解最优分配方案时,要求满足约束条件前提下,产品加工的机会成本为零,由此使得总的加工成本为最低,并验证方案变量的最优解和调整的幅度、限度
3、伏格尔法
算法步骤:
1、算出各行各列中最小元素和次小元素的差额,并标出差额最大的(若几个差额同为最大,则可任取其一)。
2、在差额最大的行或列中的最小元素处填上尽可能大的数。
3、对未划去的行列重复以上步骤,直到得到一个初始解。
实例分析:
例:某公司有三个加工厂A1,A2,A3 生产某产品,每日的产量分别为7T,4T,9T,该公司把这些产品分别运往四个销售点B1,B2,B3,B4,各销售点的每日销量分别为3T,6T,5T,6T。从各工厂到各销售点的单位运价如表1所示。问该公司如何调运产品,才能在满足各销售点需要量的前提下,使总费用最少?

第一步:求各行各列最小和次小元素的差值。
在表2中,各行的差值分别为0,1,1,各列的差值分别为2,5,1,3。可见第二列差值最大,首先考虑第二列,在第二列中最小的cij 为c32=4,令x32=min{6,9}=6,第二列饱和,划去该列。
第二步:求余下的各行各列最小和次小元素的差值。
对剩下的方格重新计算各行各列的差值,各行差值分别为0,1,2,各列差值分别为2,1,3,第四列差值最大,在第四列中,最小的cij为c34 = 5,令x34=min{6,9-6}=3,于是第三行饱和,划去第三行。
第三步:重复上述过程。
可得其他基变量的值为:x21 = 3,x13 = 4,x23 = 1,x14 = 3。如下表

此例的解所对应的 Z=1×3 4×6 3×5 10×2 8×1 5×3=85。