
平面上:在△ABC中,AB⊥AC,AD⊥BC,D为.垂足,则AB2=BD•BC,该结论称为射影定理.
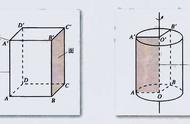
空间中,在三棱锥A﹣BCD中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,则

设A为平面上一点,过A的斜线AO在面上的身影为AB,AC为面上的一条直线,那么∠OAC,∠BAC,∠OAB,三角的余弦关系为:cos∠OAC=cos∠BAC·cos∠OAB



平面上:在△ABC中,AB⊥AC,AD⊥BC,D为.垂足,则AB2=BD•BC,该结论称为射影定理.
空间中,在三棱锥A﹣BCD中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,则

设A为平面上一点,过A的斜线AO在面上的身影为AB,AC为面上的一条直线,那么∠OAC,∠BAC,∠OAB,三角的余弦关系为:cos∠OAC=cos∠BAC·cos∠OAB














Copyright © 2018 - 2021 www.yd166.com., All Rights Reserved.