本文为 AI 研习社编译的技术博客,原标题 :
The 5 Clustering Algorithms Data Scientists Need to Know
作者 | George Seif
翻译 | 邓普斯•杰弗、arnold_hua、小Y的彩笔
校对 | 邓普斯•杰弗 审核| Lam-W 整理 | 菠萝妹
原文链接:
https://towardsdatascience.com/the-5-clustering-algorithms-data-scientists-need-to-know-a36d136ef68
聚类算法是机器学习中涉及对数据进行分组的一种算法。在给定的数据集中,我们可以通过聚类算法将其分成一些不同的组。在理论上,相同的组的数据之间有相同的属性或者是特征,不同组数据之间的属性或者特征相差就会比较大。聚类算法是一种非监督学习算法,并且作为一种常用的数据分析算法在很多领域上得到应用。
在数据科学领域,我们利用聚类分析,通过将数据分组可以比较清晰的获取到数据信息。今天我们来看看,作为数据科学家需要知道并掌握的五种比较比较流行的聚类算法。
k-means 聚类算法
K-means 聚类算法 可能是大家最为熟悉的聚类算法。它在许多的工业级数据科学和机器学习课程中都有被讲解。并且容易理解和实现相应功能的代码 。 比如以下的图片:

k-means聚类
首先,我们确定要聚类的数量,并随机初始化它们各自的中心点。为了确定要聚类的数量,最好快速查看数据并尝试识别任何不同的分组。中心点是与每个数据点向量长度相同的向量,是上图中的“x”。
通过计算当前点与每个组中心之间的距离,对每个数据点进行分类,然后归到与距离最近的中心的组中。
基于迭代后的结果,计算每一类内,所有点的平均值,作为新簇中心。
迭代重复这些步骤,或者直到组中心在迭代之间变化不大。您还可以选择随机初始化组中心几次,然后选择看起来提供最佳结果。
k-means的优点是速度非常快,因为我们真正要做的就是计算点和组中心之间的距离;计算量少!因此,它具有线性复杂性o(n)。
另一方面,k-means有两个缺点。首先,您必须先确定聚类的簇数量。理想情况下,对于一个聚类算法,我们希望它能帮我们解决这些问题,因为它的目的是从数据中获得一些洞察力。k-均值也从随机选择聚类中心开始,因此它可能在算法的不同运行中产生不同的聚类结果。因此,结果可能不可重复,缺乏一致性。
K中位数是与K均值相关的另一种聚类算法,除了不使用平均值重新计算组中心点之外,我们使用组的中位数向量。这种方法对异常偏离值不太敏感(因为使用了中值),但对于较大的数据集来说要慢得多,因为在计算中值向量时,每次迭代都需要排序。
Mean-Shift 聚类
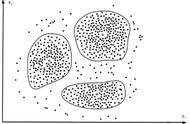
Mean-shift 聚类是一个基于滑窗的算法,尝试找到数据点密集的区域。它是一个基于质心的算法,也就是说他的目标是通过更新中心点候选者定位每个组或类的中心点,将中心点候选者更新为滑窗内点的均值。这些候选滑窗之后会在后处理阶段被过滤,来减少临近的重复点,最后形成了中心点的集合和他们对应的组。查看下面的说明图。

单滑窗的 Mean-Shift 聚类
为了解释 mean-shift,我们将考虑一个二维空间中的点集,像上图所示那样。我们以一个圆心在C点(随机选择)的圆形滑窗开始,以半径 r 作为核。Mean shift 是一个爬山算法,它每一步都迭代地把核移动到更高密度的区域,直到收敛位置。
在每次迭代时,通过移动中心点到滑窗中点的均值处,将滑窗移动到密度更高的区域(这也是这种算法名字的由来)。滑窗内的密度与在其内部点的数量成正比。很自然地,通过将中心移动到窗内点的均值处,可以逐步的移向有个高的密度的区域。
我们继续根据均值来移动滑窗,直到有没有哪个方向可以使核中容纳更多的点。查看上面的图,我们一直移动圆圈直到密度不再增长。(即窗内点的数量不再增长)。
用很多滑窗重复1-3这个过程,直到所有的点都包含在了窗内。当多个滑动窗口重叠时,包含最多点的窗口将被保留。然后,根据数据点所在的滑动窗口对数据点进行聚类。
下图展示了所有滑动窗口从端到端的整个过程。每个黑色的点都代表滑窗的质心,每个灰色的点都是数据点。

Mean-Shift 聚类的全部过程
与 K-means 聚类不同的是,Mean-Shift 不需要选择聚类的数量,因为mean-shift 自动发现它。这是一个很大的优点。事实上聚类中心向着有最大密度的点收敛也是我们非常想要的,因为这很容易理解并且很适合于自然的数据驱动的场景。缺点是滑窗尺寸/半径“r“的选择需要仔细考虑。
基于密度的带噪声的空间聚类的应用(DBSCAN)
DBSCAN 是一个基于密度的聚类算法,与 mean-shift 相似,但是有几个值得注意的优点。查看下面这个花哨的图片,我们开始吧!