聚类分析原理及步骤,聚类分析用哪种分析方法

在本篇，我会重点说说无监督学习的算法。在监督学习的算法中，关于线性回归部分，之前在《（万字干货）如何训练优化“AI神经网络”模型？》中有提到，而半监督学习和强化学习的相关内容，我会在以后的文章中，再和大家娓娓道来。

2. 我们为什么需要算法，价值几何？

无监督学习是机器学习的一种方法，算法就是实现无监督学习的工具，更是无监督学习的核心。无监督学习的目标是发现数据中的内在关系，而算法的设计和选择直接决定了这一目标能否实现以及实现的效率和效果。

在无监督学习中，算法的价值不言而喻，主要凸显在以下几处。

【数据探索与模式发现】

我们之前多次提到，无监督学习可以发现数据中的潜在结构和模式，帮助理解数据的内在特性。

但我们从未细细推敲过，无监督学习是如何发现数据中的结构和模式的。而算法，就是开启这个盲盒的钥匙。数据探索与模式发现的全部奥秘，都在算法之中。

【数据预处理】

从我之前写的几篇关于数据集的文章中可知，我们在AI训练之前，需要对数据进行预处理，这是一个非常关键的步骤。

那么，问题又来了，我们该如何高效完成数据预处理的任务呢？答案是：善用算法。

比如，在实际情况中，我们拿到的初始数据往往包含缺失值、异常值或噪声。而聚类或密度估计这类算法，可以帮助识别和处理这些不完整的或异常的数据点，从而提高数据质量。

【特征提取】

在特征提取方面，算法可以帮助识别数据中的重要特征，为后续的监督学习任务或其他分析提供更有用的数据表示。就像考试前，已经有一位学神帮你勾出了重要知识点，助你逢考必过。

再有，像是降维算法，也是无监督学习中常用的特征提取算法，它通过降低数据的维度，保留主要信息的同时减少冗余。这有助于简化数据表示，提高计算效率，并减少过拟合的风险。

【降低标注成本】

通俗点说，算法还有一大价值，就是省钱省时省人力。在传统的监督学习中，模型的训练通常需要大量带有标签的数据，而这一标注过程既费时又费力。

无监督学习之所以能够在大多数情况下利用未标注的大规模数据进行训练，是因为算法在背后起着关键作用。

特别是当我们要涉足一个新领域时，获取足够数量的标注数据可能是一项昂贵且耗时的工程。这该如何解决？答案还是：善用算法。

我们通常会让算法先在一个相关领域进行无监督学习，这样AI模型就可以学到通用的特征和表示，就可以减少对于新领域标注数据的需求，也就有效地降低了在新任务上进行标注所需的成本，加速了模型的部署和应用。

纵观算法价值，我总结了4个方面，分别是“数据探索与模式发现”、“数据预处理”、“特征提取”和“降低标注成本”。也许还有不完善之处，但力求可以帮助各位看官理解算法的重要性，即便只获一二，都值得欢喜。

1. 聚类算法的基本概念

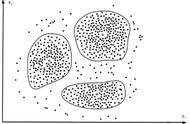
在无监督学习中，聚类算法是一类将数据集分成若干个群组的算法。这些群组称为“簇”。每个簇内的数据点彼此之间相似度较高，而不同簇的数据点相似度较低。

聚类算法要做的就是，在没有任何预先标注的情况下，将相似的数据点归为一簇，将不相似的数据点划分到不同的簇中。

基于聚类算法，我们可以更容易地理解数据的分布、发现数据中的异常值，解决数据压缩、图像分割、市场细分等各类问题。

常见的聚类算法包括：K均值聚类（K-Means Clustering）、层次聚类（Hierarchical Clustering）、DBSCAN（Density-Based Spatial Clustering of Applications with Noise）、高斯混合模型（Gaussian Mixture Model，GMM）等。

其中，K均值聚类算法（通常称为K-means算法）的早期版本由Stuart Lloyd在1957年提出。他的研究是为了优化通信系统中的信号传输。

后来，该算法被MacQueen在1967年重新发现，他将其用于数据分析领域。MacQueen在他的论文中正式描述了K-means算法，并首次使用了“K-means”这个名称。

层次聚类的概念最早由J.L. Ward于1963年提出，该方法特别关注于最小化整个数据集的总方差，通过这种方式来形成层次聚类的结构。

而DBSCAN，首次出现在1996年的论文中，由Martin Ester等人共同提出的。它能够在有噪声的数据集中发现任意形状的簇，并且能够识别并处理噪声点。

至于高斯混合模型，有着更早的演进过程，其概念可以追溯到19世纪，但具体由谁提出就不得而知了。

本篇，我们就重点来说说聚类算法中的K均值聚类和层次聚类。

2. K均值聚类（K-Means Clustering）

K均值聚类（K-Means Clustering）是一种经典的聚类算法，其基本原理是将数据点分为K个簇，每个簇由簇中心（通常是簇内所有点的均值）表示。

所以，K-Means算法涉及到簇中心的计算，对于第i个簇，其簇中心（质心）的计算公式为：

K均值聚类的目标是最小化簇内平方误差，即找到K个簇，使每个数据点与其所属簇中心的距离之和最小。目标函数的数学公式是：

从公式可见，E值越小则簇内数据（样本）相似度越高。K-Means算法通过迭代更新簇中心，不断优化这个目标函数，来达到更好的聚类效果。

现在，我们已知数学公式，可以进一步了解K-Means算法是如何实现迭代优化的？

1. K-Means算法是在不断迭代中找到最优解的，大致步骤如下：
2. 初始化：随机选择K个数据点作为初始簇中心。
3. 分配数据点：对于数据集中的每个数据点，计算其与各个簇中心的距离，并将其分配到距离最近的簇中心所在的簇。
4. 更新簇中心：计算每个簇内所有数据点的均值（或其它形式的中心），将其作为新的簇中心。这个均值可以是算术平均值、几何平均值、中位数等。
5. 重新计算误差：重新计算每个簇内数据点到簇中心的距离，并计算总的平方误差。
6. 迭代：重复步骤(2)—(4)，直到满足停止条件。停止条件可以是簇中心的变化小于某个阈值，或是达到预设的最大迭代次数，又或是误差函数的减少小于某个值。

从K-Means算法的步骤中，我们能发现该算法对初始簇中心的选择敏感，不同的初始中心可能导致完全不同的聚类结果。

3. K均值聚类算法能解决什么问题？

我们不能让算法只停留在理论层面，我们还需要让K-Means算法可以解决一些实际问题。

在实际场景中，K-Means算法可以解决聚类问题，通俗点说，可以帮我们完成大量数据的分类任务。比如：市场细分、图像分割、文档分组、异常检测或者数据压缩等。

【K-Means算法-客户分群】

假设公司的CRM系统中有大量的客户交易信息，比如购买时间、购买金额、购买频率、购买商品类型等。我们的目标是根据这些数据将客户分为不同的群体，以便更好地定制营销策略。

这时候采用K-Means算法就可以高效解决这个问题。

最开始，我们需要从CRM系统中提取相关的客户交易信息，做好数据准备。原始数据的数量和质量是影响最终目标成败的关键。

然后，我们需要对提取到的数据进行预处理。对数据进行清洗，处理缺失值、异常值，并可能进行归一化或标准化处理，以便于算法能够更好地处理这些数据。

K-Means算法需要预先指定簇的数量K，我们需要选择合适的K值。可以尝试不同的K值，并使用如肘部法则（Elbow Method）或轮廓系数（Silhouette Score）来完成选择。

然后是初始化簇中心。随机选择K个数据点作为初始簇中心，再使用选择的 K 值执行 K-Means 算法，将客户分为 K 个簇，每个簇代表一个客户群体。执行K-Means算法的过程中会涉及到多次的更新迭代。

此后，我们需要评估聚类结果，还需要对每个簇进行分析，了解每个客户群体的特征。这可能涉及到购买习惯、活跃度、商品偏好等方面的特征，还可以使用可视化工具展示每个簇的特征分布。

当我们一旦确定了最佳的聚类结果，就可以根据不同的客户群体制定个性化的营销策略。例如，对高价值客户采取个性化服务，对潜在回流客户采取促销活动，对频繁购买的客户群提供额外奖励等。

在整个假设案例的过程中，我们可以发现K-Means算法落地到实际应用场景中，能解决什么样的问题。

我们可以利用K-Means算法对客户交易数据进行聚类，从而实现客户群体的细分，帮助公司高层和市场销售人员更好地理解客户群体，市场部门可以制定更加精准和有效的营销策略，提高公司ROI，提高客户满意度，提高公司业务效益。

4. 层次聚类（Hierarchical Clustering）

层次聚类算法（Hierarchical Clustering）是一种基于数据点之间的相似性进行聚类的算法。与K-Means算法不同，层次聚类不需要预先指定簇的数量，它通过逐步合并或分裂现有的簇来构建一个簇的层次结构。

根据数据集的划分是“自底向上”的聚合策略，还是“自顶而下”的分拆策略，层次聚类算法可以进一步分为凝聚的层次聚类算法AGNES（AGglomerative NESting）和分裂的层次聚类算法DIANA（DIvisive ANAlysis）。

初始时，AGNES将每个对象自成一簇，之后这些簇依照某一种准则逐步合并。DIANA则以相反的方法处理，初始时将所有对象归为同一类簇，然后依据某种原则将该簇逐渐分裂。