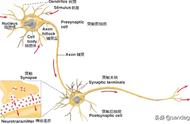
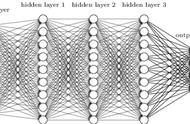
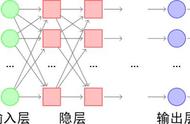
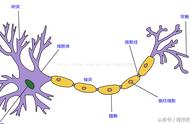
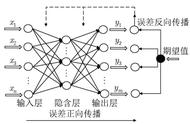
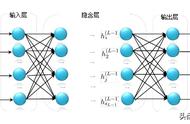
某个神经元节点的输入信号:

某个神经元节点的输出信号:

神经网络的预测值的损失函数/代价函数为:

注1:损失函数LossFunction、误差函数ErrorFunction、代价函数CostFunction,及其缩写L、E、C表达的是同一个函数。
注2:损失函数里的系数1/2,仅仅是为了令函数求导后的系数为1,为了方便计算而设定的,没有实际意义。
4 反向传播
4.1 算法思路
为了能够得到一个优质的神经网络模型,我们需要求模型的两类参数w和b的最优值,以达到令损失函数值最小的目标。
显而易见的,对于这个L的最优化问题,我们可以考虑使用求偏导数的方法,并利用梯度下降法逐步逼近参数w和b的最优解。
但是由于神经网络结构复杂、参数多,导致传统的偏导数和梯度下降法无法直接被使用。直至反向传播算法应运而生,它大大提高了求解神经网络模型的最优化参数的效率,使得神经网络实现了从理论到工业应用的跨越,也掀起了学习和使用神经网络的热潮。
反向传播算法:首先利用损失函数求得模型的最终误差。接着再将误差自后向前层层传递,获取每个神经元的误差。最后将每层每个神经元的误差对w和b求偏导,迭代获取的w和b的最优解,从而构建损失函数最小的最优神经网络模型。当然,和梯度下降法类似,神经网络也需要经过多次迭代,才能够逼近并获得最优模型。
注:反向传播算法能够提高计算效率的两个因素:一是运算过程的向量化,二是能够实现分布式计算。
4.2 求误差δ
我们对任意神经元上的误差δ作出如下定义: