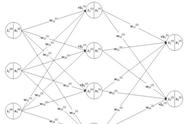
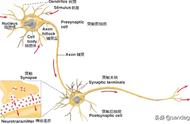
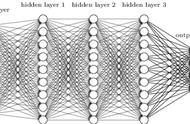
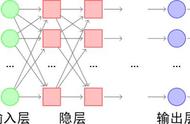
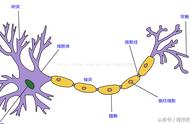
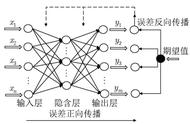
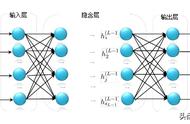
研究证明:神经元网络拓扑结构可以逼近任意非线性函数(国外论文数学论证了的,就当它具有这个功能就行了,仿生学厉害呀,仿造人脑神经元间的信息传递)。而且观察到神经元网络为多输入的并行结构,能同时输入不同类型的信息进行处理并给出输出,高效而迅速。
有了万能的淘宝,呕不,万能的模具。还差一个美工刀来雕琢修改了。倒是有很多种偏差修正函数,这里提一种我熟悉也较为通用(通用始终比不上专用的喽)的修正判定函数吧。
二次型性能修正:和最小二乘法的思想相似,取偏差的平方差构成2次函数。
简单的例子:有一根绳子长度为x米,需要另外剪一根和它长度一样的绳子。第一次剪了y1米,y1>x长了就需要剪短。第二次再修正剪短一节n1米,当前的绳子长y2=y1-n1,发现y2短了需要增长。第三次再修正增加一节n2米...以此类推,不断的逼近目标,使偏差趋于零。
最小二乘法:我们都知道一元二次函数

的曲线是一个“U”形,如下图所示:

一元二次函数曲线
可以观察到,U形最底部与x相交处函数值最小,趋近于零。由梯度下降法求解极小值思想,向函数增大的反方向或者函数减小的同方向迈步,而函数的变化方向可以通过求导得到,在交点左侧导数小于零,右侧导数大于零。
梯度下降法:导数为正函数正在增大,外部修正调节效果变坏,应反向调节使其减小;导数为负函数正在减小外部修正修正调节效果变好,函数正在减小趋近于零,保存当前调节。通过不断的正反向梯度调节,最终逐渐逼近于导数为零时,纯2次函数的导数为零点即偏差为零点。从而达到学习调整权值逐渐趋近期望目标,使偏差逼近零。(不断的剪短或增加绳子的长度,逐渐的趋近于目标值,偏差趋于零)。
于是借助于其特性,我们假定当前值和目标值得偏差为ek=y-x,设函数

,就可以确定该用美工刀挖一刀或者加点材料了。