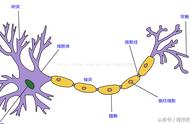
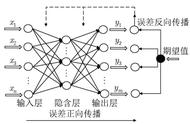
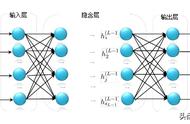
反向传播:求导,或者偏导,调整各层间的权值。隐含层到输出层连接权值修正值:

输入层到隐含层连接权值修正值:

式中p为学习速率,p一般取0~1之间的值稳定。(-1)是由梯度下降法得来的,导数>0时需反向控制,导数<0时需保持控制,所以乘以-1正好抵消满足。则下一次隐含层到输出层的连接权值Wjk和输入层到隐含层的连接权值Wij分别为:
Wjk(n 1)=Wjk(n) △Wij
Wij(n 1)=Wij(n) △Wjk
为了避免权值的学习过程发生振荡、收敛速度慢,需要考虑上次权值变换对本次权值变换的影响,即加入动量因子α(为了一定程度上避免陷入局部凹坑)。此时权值为:
Wjk(n 1)=Wjk(n) △Wjk α(Wjk(n)-Wjk(n-1))
Wij(n 1)=Wij(n) △Wij α(Wij(n)-Wij(n-1))
通常而言0<α<1,大小合适可以振荡越过局部凹坑,太大就可能振荡的无法趋近于全局最优解,太小无法振荡越出局部凹坑,但通常而言,一般的函数就够了。由此可见反向学习算法还是挺重要的,所以这把美工刀需要选择好。
参考书籍----《智能控制》-刘金琨
---------------------------------------------分割线---------------------------------------------
终于,数学讨论结束了。下面我们进行试验论证,使用Java实现BP神经网络算法。
Java Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
import java.util.Scanner;
public class BpNet
{
private static final int IM = 1; //输入层数量
private static final int RM = 8; //隐含层数量
private static final int OM = 1; //输出层数量
private double learnRate = 0.55; //学习速率
private double alfa = 0.67; //动量因子
private double Win[][] = new double[IM][RM]; //输入到隐含连接权值
private double oldWin[][] = new double[IM][RM];
private double old1Win[][] = new double[IM][RM];
private double dWin[][] = new double[IM][RM];
private double Wout[][] = new double[RM][OM]; //隐含到输出连接权值
private double oldWout[][] = new double[RM][OM];
private double old1Wout[][] = new double[RM][OM];
private double dWout[][] = new double[RM][OM];
private double Xi[] = new double[IM];
private double Xj[] = new double[RM];
private double XjActive[] = new double[RM];
private double Xk[] = new double[OM];
private double Ek[] = new double[OM];
private double J = 0.1;
public static void main(String[] arg)
{
BpNet bpNet = new BpNet();
bpNet.train();
Scanner keyboard = new Scanner(System.in);
System.out.println("Please enter the parameter of input:");
double parameter;
while((parameter = keyboard.nextdouble()) != -1)
System.out.println(parameter "*2 23=" bpNet.bpNetOut(parameter / 100.0)[0] * 100.0);
}
public void train()
{
double y;
int n = 0;
//初始化权值和清零//
bpNetinit();
System.out.println("training...");
while(J > Math.pow(10, -17))
{
for(n = 0; n < 20; n )
{
y = n * 2 23; //逼近对象
//前向计算输出过程//
bpNetForwardProcess(n / 100.0, y / 100.0);
//反向学习修改权值//
bpNetReturnProcess();
}
}
//在线学习后输出//
for(n = 0; n < 20; n )
{
y = n * 2 23; //逼近对象
System.out.printf("%.1f ", y);
System.out.printf("%f ", bpNetOut(n / 100.0)[0] * 100.0);
System.out.println("J=" J);
}
System.out.println("n=20 " "Out:" this.bpNetOut(20 / 100.0)[0] * 100);
}
//
// BP神经网络权值随机初始化
// Win[i][j]和Wout[j][k]权值初始化为[-0.5,0.5]之间
//
public void bpNetinit()
{
//初始化权值和清零//
for(int i = 0; i < IM; i )
for(int j = 0; j < RM; j )
{
Win[i][j] = 0.5 - Math.random();
Xj[j] = 0;
}
for(int j = 0; j < RM; j )
for(int k = 0; k < OM; k )
{
Wout[j][k] = 0.5 - Math.random();
Xk[k] = 0;
}
}
//
// BP神经网络前向计算输出过程
// @param inputParameter 归一化后的理想输入值(单个double值)
// @param outputParameter 归一化后的理想输出值(单个double值)
//
public void bpNetForwardProcess(double inputParameter, double outputParameter)
{
double input[] = {inputParameter};
double output[] = {outputParameter};
bpNetForwardProcess(input, output);
}
//
// BP神经网络前向计算输出过程--多个输入,多个输出
// @param inputParameter 归一化后的理想输入数组值
// @param outputParameter 归一化后的理想输出数组值
//
public void bpNetForwardProcess(double inputParameter[], double outputParameter[])
{
for(int i = 0; i < IM; i )
{
Xi[i] = inputParameter[i];
}
//隐含层权值和计算//
for(int j = 0; j < RM; j )
{
Xj[j] = 0;
for(int i = 0; i < IM; i )
{
Xj[j] = Xj[j] Xi[i] * Win[i][j];
}
}
//隐含层S激活输出//
for(int j = 0; j < RM; j )
{
XjActive[j] = 1 / (1 Math.exp(-Xj[j]));
}
//输出层权值和计算//
for(int k = 0; k < OM; k )
{
Xk[k] = 0;
for(int j = 0; j < RM; j )
{
Xk[k] = Xk[k] XjActive[j] * Wout[j][k];
}
}
//计算输出与理想输出的偏差//
for(int k = 0; k < OM; k )
{
Ek[k] = outputParameter[k] - Xk[k];
}
//误差性能指标//
J = 0;
for(int k = 0; k < OM; k )
{
J = J Ek[k] * Ek[k] / 2.0;
}
}
//
//BP神经网络反向学习修改连接权值过程
//
public void bpNetReturnProcess()
{
//反向学习修改权值//
for(int i = 0; i < IM; i ) //输入到隐含权值修正
{
for(int j = 0; j < RM; j )
{
for(int k = 0; k < OM; k )
{
dWin[i][j] = dWin[i][j] learnRate * (Ek[k] * Wout[j][k] * XjActive[j] * (1 - XjActive[j]) * Xi[i]);
}
Win[i][j] = Win[i][j] dWin[i][j] alfa * (oldWin[i][j] - old1Win[i][j]);
old1Win[i][j] = oldWin[i][j];
oldWin[i][j] = Win[i][j];
}
}
for(int j = 0; j < RM; j ) //隐含到输出权值修正
{
for(int k = 0; k < OM; k )
{
dWout[j][k] = learnRate * Ek[k] * XjActive[j];
Wout[j][k] = Wout[j][k] dWout[j][k] alfa * (oldWout[j][k] - old1Wout[j][k]);
old1Wout[j][k] = oldWout[j][k];
oldWout[j][k] = Wout[j][k];
}
}
}
//
// BP神经网络前向计算输出,训练结束后测试输出
// @param inputParameter 测试的归一化后的输入值
// @return 返回归一化后的BP神经网络输出值,需逆归一化
//
public double[] bpNetOut(double inputParameter)
{
double[] input = {inputParameter};
return bpNetOut(input);
}
//
// BP神经网络前向计算输出,训练结束后测试输出
// @param inputParameter 测试的归一化后的输入数组
// @return 返回归一化后的BP神经网络输出数组
//
public double[] bpNetOut(double[] inputParameter)
{
//在线学习后输出//
for(int i = 0; i < IM; i )
{
Xi[i] = inputParameter[i];
}
//隐含层权值和计算//
for(int j = 0; j < RM; j )
{
Xj[j] = 0;
for(int i = 0; i < IM; i )
{
Xj[j] = Xj[j] Xi[i] * Win[i][j];
}
}
//隐含层S激活输出//
for(int j = 0; j < RM; j )
{
XjActive[j] = 1 / (1 Math.exp(-Xj[j]));
}
//输出层权值和计算//
double Uk[] = new double[OM];
for(int k = 0; k < OM; k )
{
Xk[k] = 0;
for(int j = 0; j < RM; j )
{
Xk[k] = Xk[k] XjActive[j] * Wout[j][k];
Uk[k] = Xk[k];
}
}
return Uk;
}
}