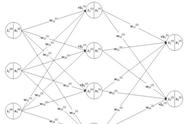
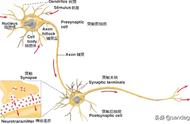
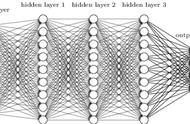
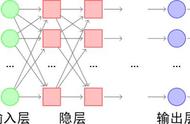
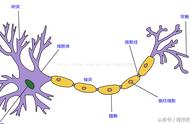
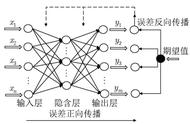
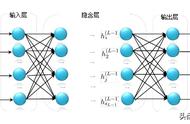
神经网络结构
输入的层数(Xi):
需要选取对系统对象影响较大的变量,例如 逼近函数
y(k)=sin(5x) y(k-1)^2;
可以基本确定影响因素为:
输入样本1: Sin(5x)或者x
输入样本2: y(k-1)
这需要一定的练习才能更好的掌握,也就是输入的是一些教师信号(由什么可以及应该得到什么),通过不断的调整各个权值来逐步的逼近这个函数规律。
输入(Wij)输出(Wjk)权值:
一般取[0,1]或[-1,1]区域内的随机值,C语言中使用(rand(srand(time(NULL))00)/1000.0以时间作种的随机数变换得到,具体为什么要取这之间的权值,还不太清楚,计算的方便可能是影响因素之一。
隐含层数Xj:
隐含层书上所说基本靠经验试凑确定,还有是输入层数 输出层数 值,一般我们取5层就可以满足要求,隐含层数的增加可以更加精准的逼近目标函数,提高网络的精度。
输出层数Xk:
所求对象的输出,需要想要得到的数值。 例如 y(k)=sin(5x) y(k-1)^2;则对象输出为yn(k),后边根据理想教师信号的输出y(k)与网络计算的输出做误差运算来修正权值逼近理想输出。
隐含层神经元的输入为所有输入的加权之和:

即例如" X1j=W11*X1 W21*X2 W31*X3 ... Wi1*Xj "以此类推。
隐含层神经元输出Xj'采用S型函数激发Xj得:

隐含层的激活函数选择:
常用的是S型的对数或正切激活函数以及线性函数,S型函数具有非线性放大系数功能,它可以把输入从负无穷大到正无穷大的信号变换成-1到1之间输出,对较大的输入信号,放大系数较小,而对较小的输入信号,放大系数则较大,所以采用S型激活函数可以处理和逼近非线性的输入、输出关系。如果在输出层采用S型函数,输出则被现在到一个很小的范围,若采用线性激活函数,则可使网络输出任何值。所以当网络的输出没有限制时在隐含层采用S型激活函数,而输出层采用线性激活函数。
输出层神经元为所有隐含层输出的加权之和:

网络输出与理想输出误差为:
e(n)=XLk(n)-Xk(n) (理想输出-网络输出)
其中k为第几个输出神经元,n为计算值的第几次。
由最小二乘法思想,引入误差性能指标函数: