多个总体参数的判断
如果需要对更多的总体参数进行推断或者需要研究多个变量之间的关系,则需要方差分析的思想和内容。
前面4章,我们学习到统计数据的类型有分类数据、顺序数据和数值型数据。在实际运用中,我们主要研究的是分类数据和数值型数据。数据类型的改变会导致研究方法的改变,本节我们介绍的研究多个总体参数的推断方法分别是研究分类型自变量对数值型因变量影响的方差分析和研究分类型自变量对分类型因变量影响的卡方检验
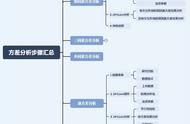
什么是方差分析
统计学的方法,心理,医药,管理,生物,都有应用。
1.检验多个总体均值是否相等
通过分析数据的误差判断各总体均值是否相等2.研究分类型自变量对数值型因变量的影响3.单因素方差分析:涉及一个分类的自变量


方差分析中的相关术语
1.因素或因子
所要检验的对象
要分析类目对投诉次数是否有影响,类目是要检验的因素或因子2.水平或处理
因子的不同表现
服装、电子产品、彩妆、医药就是因子的水平
3.观察值
在每个因素水平下得到的样本数据每个行业被投诉的次数就是观察值
4.试验
这里只涉及一个因素,因此称为单因素四水平的试验
5.总体
因素的每一个水平可以看作是一个总体比如服装、电子产品、医药、彩妆就可以看作是四个总体
6.样本数据
被投诉次数可以看作是从这是个总体中抽取的样本数据

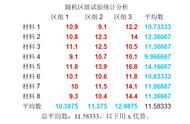
3.仅从散点图上观察还不能提供确信的证据证明不同行业被投诉的次数之间有显著差异这种差异也有可能是由于抽样的随机性造成的
4.需要有更准确的方法来检验这种差异是否显著,也就需要对数据进行方差分析之所以叫方差分析,是因为虽然我们感兴趣的是均值,但是在判断均值之间是否有差异时则需要借助方差
误差分解
1.随机误差和系统误差
a.随机误差:因素的同一水平(同一总体)下,样本各观察值之间的差异。比如同一类目下不向公司被投诉次数是不同的。
这种差异可以看成是随机因素的影响
b.系统误差:因素的不同水平下(不同总体)下,各观察值之间的差异。比如不同类目之间的
被投诉次数之间的差异。
这种差可能是由于抽样的随机性造成的,也可能是由于行业本身所造成的,后者所形成的误差是由系统性因素造成的,称为系统误差。
2.组内方差和组间方差
a.组内方差
因素的同一水平(同一总体)下样本数据的方差组内方差只包含随机误差
b.组间方差
因素的不同水平(不同总体)下样本数据的方差组间方差既包括随机误差,也包括系统误差
误差分析
1.若不同类目对投诉次数没有影响,则组间误差中只包含随机误差,没有系统误差。这时,组间误差与组内误差经过平均后的数值就会很接近,它们的比值就会接近1/
2.若不同类目对投诉次数有影响,在组间误差中除了包含随机误差外,还会包含有系统误差,这时组间误差平均后的数字就会大于组内误差平均后的数值,它们的比值就会大于1
3.当这个比值大到某种程度时,就可以说不同水平之间存在着显著差异,也就是自变量对因变量有影响
方差分析中的基本假定
1.每个总体都应该服从正态分布对于因素的每一个水平,其观察值都是来自服从正态分布总体的简单随机样本比如,每个类目被投诉的次数必需服从正态分布
2.各个总体的方差必须相同
各组观察数据是从具有相同方差的总体中抽取的比如,四个类目被投诉次数的方差都相等
3.观察值是独立的
比如,每个类目被投诉的次数与其他行业被投诉的次数独立