有没有一个好的方法来学习理解方差分析,条理清晰,理解容易呢?
方差分析,是析因试验,就是分析效应的过程,所以通过效应,就可以轻松解决方差分析的学习问题。
方差分析,可以用这样的模型来描述
Yij =μ αi eij
αi 就是不同的效应,比如,区组效应,品种效应,A因素效应等等,
记住这3句话,你就学会方差分析了:
①每一个效应都对应一个平均数,是与总平均数的离差
②每一个效应相关的观测值的数量就是要跟离差相乘的系数
③每一个效应内部平均数的数量-1就是这个效应的自由度
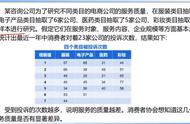
示例


对应理解这3句话
①每一个效应都是一个平均数
区组有区组平均数,材料有材料平均数
每一个效应都是效应平均数与总平均数的离差
区组1平均数-总平均,
8*(10.3875-x)²
材料1平均数-总平均
3*(10.73333-x)²
②每一个效应相关的观测值的数量就是要跟离差相乘的系数
区组1有8个观测值,所以8*(10.3875-x)²
材料1有3个观测值,所以3*(10.73333-x)²
③每一个效应内部平均数的数量-1就是这个效应的自由度
区组效应内部共有3个区组平均数,分别是区组1、区组2、区组3,所以方差分析的区组间自由度是3-1=2。
材料效应内部有8个材料平均数,所以,方差分析材料间自由度是8-1=7。


F测验,自己去组合就是了,需要检验哪个效应就构建哪个效应的F测验,比如:
A效应测验:
分子是:6.222222222÷(3-1)
分母是:7.77811111÷16
,