决策树模型理论介绍
- 决策树算法是一种归纳分类算法,它通过对训练集的学习,挖掘出有用的规则,用于对新集进行预测
- 非参数学习算法。对每个输入使用由该区域的训练数据计算得到的对应的局部模型
- 决策树归纳的基本算法是贪心算法,自顶向下递归方式构造决策树
- 在其生成过程中,分割方法即属性选择度量是关键。通过属性选择度量,选择出最好的将样本分类的属性
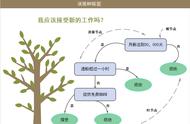
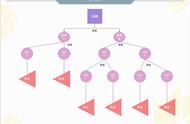
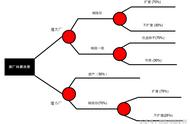
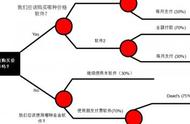
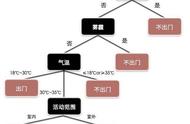
决策树算法以树状结构表示数据分类的结果。每个决策点实现一个具有离散输出的测试函数,记为分支。

决策树的结构
决策特征/属性选择- 特征选择在于选取对训练数据具有分类能力的特征
- 选择特征的准则:
- 信息增益—ID3算法
- 信息增益比—C4.5算法
- 基尼指数—CART算法
- CART同样由特征选择、树的生成及剪枝组成,即可以用于分类也可以用于回归
- CART假设决策树是二叉树,内部结点特征的取值为“是”和“否”,这样的决策树等价于递归地二分每个特征:
- 对回归树用平方误差最小化准则
- 分类树用基尼指数(Gini index)最小化准则
计算每个属性/特征的Gini指数,选择Gini最小的特征作为分类特征。

Gini指数计算
连续值属性/特征的处理- Step1 根据训练数据集中属性的值对该训练数据集进行排序
- Step2 利用其中属性的值对该训练数据集动态地进行划分
- Step3 在划分后的得到的不同的结果集中确定一个阈值,该阈值将训练数据集数据划分为两个部分
- Step4 针对这两边各部分的值分别计算它们的增益或增益比率或Gini指数,以保证选择的划分是最优的
代码详见微头条。

决策树模型编程实践