数学分析(或微积分)应该说是进入大学之后最重要的数学基础课,以后所学的很多课程都和它相关,它的概念、思想和方法已经渗透到了许多地方,所以把它学好是至关重要的。在这篇小文章里,我就结合自己的学习体会,给大家交流一下我的一些愚见。全文分为三部分,分别为“数学分析的内容”、“相关书籍”和“学*结”。限于篇幅,只能提及一些最关键的东西。

数学分析的内容
单元微积分
微积分自牛顿和莱布尼茨创立之后,再经柯西、魏尔斯特拉斯等人严格化之后,已经成为完整而成熟的学科,是研究函数理论最基本的学科,尽管或多或少这套理论有它的不足,但这也不妨碍它成为现代科学的数学基础。
准确而言,实数范围内的“数学分析”是数学专业的叫法,而“分析”是对微积分相关学科的泛称。在我国,理工科所学微积分课程一般称为“高等数学”,其间还会涉及一些空间解析几何和一点常微分方程,但其微积分内容还是包含在“数学分析”课程之内,而且要求要低一些。本文还是以数学作业的“数学分析”课程内容为准。
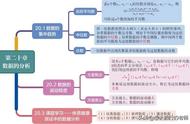
数学分析的课程内容可大致分为三部分:单元微积分、多元微积分和级数。
单元微积分要处理的就是单元函数的“极限”、“微分”和“积分”的问题。极限是贯穿整个微积分理论的概念,对它的理解和处理是至关重要的。一般都是先从离散的数列开始,再到一般的连续函数,这里会有一系列关于极限和收敛性的结论。但重中之重是要掌握极限的定义和相关的“δ-ε”语言,脱离基本定义的学习都是空中楼阁。需要注意的是,实数理论作为极限理论的基础,非数学系一般没有太多要求,但数学系的学生是必须要掌握的。
微分和导数这一块能够更加详细分析函数的性质。首先要注意的仍是概念,特别是“微分”,学过微积分的人里有一大半无法准确说出“微分”到底是个什么概念或者和导数有什么关系。这一部分最重要的内容是中值定理(费马中值定理、罗尔中值定理、拉格朗日中值定理、柯西中值定理)和泰勒展开式,还需要掌握的就是求各种函数极限,洛必达法则作为中值定理的产物,在求极限中起着重要作用。

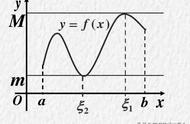
积分论首先的内容是求不定积分,也就是求导的逆运算,这里需要各种方法,如换元法和分部积分等。一般的定积分理论是黎曼奠定的基础,其间还有达布等人的贡献。关于定积分的定义也是很重要的,而关于可积性,和实数理论一样,数学系会着重要求。牛顿-莱布尼茨公式沟通了微分和积分的关系,是这一理论的灵魂所在。会求各种定积分也是这门课的内在要求。定积分也有很多重要的性质,特别的有两个重要的积分中值定理。但并不是所有函数都可以求积分,所以还需要判定反常积分是否收敛,这又是一大难点,需要掌握几个重要的判断准则。

多元微积分
多元微积分理论是单元微积分理论的自然延伸,但它又有着独特的地方。首先多元函数的极限和连续性变得复杂,能否交换求极限次序成为关键。可微与可导的关系也不再像单元函数那样直接,需要仔细处理。多元复合函数的求导法则也变得复杂起来,掌握链式法则是关键。同样,多元函数也有相应的中值定理和泰勒展开。之后对隐函数的处理也是一大难点。偏导数的应用,特别是对空间解析几何,充分显示了它的优越性。而多元函数微分学的一大重要内容就是求极值,这在之前是很难实现的。而求极值分为无条件极值和条件极值,无论是哪一种,判断法则要熟知。
而多元函数的积分理论相较单元函数而言就十分丰富了。首先是一般的多重积分,这里变量替换和积分区域的判断是关键。同样的,多重积分也有反常积分。接下来就是曲线积分和曲面积分,分别有两类,有比较固定积分方法。之后就导出了一般的格林公式和高斯公式,还有更具一般意义的斯托克公式,这部分内容和物理中的场论息息相关。再接下来就是含参积分,顾名思义,就是含有参数的积分,需要研究它的连续性、可微性和可积性,而它的一致收敛性尤其重要。这一部分也会涉及一些特殊函数,如Gamma函数和Beta函数。