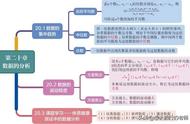
级数
级数理论是数学中比较有特色的内容,同时级数也是研究函数性质强有力的工具。级数部分大致分为数项级数、函数项级数和傅里叶级数。对于数项级数而言,判断收敛性是首要的内容,判断法则有柯西判别法、达朗贝尔判别法、拉贝判别法和积分判别法等。而对于任意项级数,还有阿贝尔判别法和狄利克雷判别法等。对于函数项级数而言,一致收敛性是最重要的内容,有一系列的判别法。一致收敛的重要性在于它可以判断函数项级数是否可以逐项求导或积分,这对于函数项级数的求和而言是至关重要的。而幂级数作为特殊的函数项级数,有许多良好的性质。
而傅里叶级数本来是傅里叶分析的一部分,一般的数学分析教材也会有所涉及。函数的傅里叶级数展开是容易的,但一个傅里叶级数收敛性的判断是不容易的。傅里叶级数的良好性质使得它不仅在数学上很有用,在物理等学科上也有重要作用。

相关书籍
无论你是哪所大学,用的什么教材,我想辅助的书籍都是必不可少的。好的书籍可你帮助学习,不好的书籍真的可以毁了你的学习。
首先菲赫金哥尔茨的三卷本巨著《微积分学教程》是非常值得推荐的,毕竟是大家之作,所以非常具有参考的价值。《微积分学教程》兼顾了理论和应用,内容十分丰富,称得上是博大精深。但缺点也是不可避免的,首先是篇幅过大,其次由于成书已久,观点可能有些老,所以同学们应根据自己需要去读。陈天权的《数学分析讲义》就是传说中的地狱级难度了,如果没有秒*一般教材的能力,不建议轻易尝试此书,特别是初学者。不过课后习题还是非常不错的,认真做一做对提高水平很有好处,作者也在前言写了很多关于数学学习的想法,很有借鉴意义。另外诸如卓里奇的《数学分析》、张筑生的《数学分析新讲》、Rudin的《数学分析原理》都还不错,可以借鉴。教材没有最好的,只有适合自己的,应该根据自己的需求来选择,所以不建议一开始就看难的,这是不利于打好基础的。数学分析不乏其他好教材,但难以一一介绍了。


学数学分析我个人觉得很不错的习题书是裴礼文的《数学分析中的典型问题和方法》,这是一本大块头的综合习题书,很难全部读完。书中习题非常丰富,像一本百科全书一般,正文的题有详细解答,课后习题只有提示,而且基本上都不怎么简单。能认真做下来的话我相信数学分析水平应该算是很不错了。不过不能理解的是,书中竟然没有不定积分的题。如果有大神觉得还不够过瘾,可以试试周民强的《数学分析习题演练》,难度如同陈天权的教材一样变态,解答都是长篇大论式的,适合研究性学习。不过缺点非常明显,书中印刷错误真的很多,有些论证也有些问题,希望以后能修正。吉米多维奇名声特别大,不过个人不建议去刷,很多题都过于复杂,有些钻牛角尖的嫌疑了。另外诸如谢惠民的《数学分析习题课讲义》也很不错,有很多启发性的题型,可惜课后题没答案,需要花功夫去做,其实这也并不是什么坏事。