分位数-分位数图(Quantile-Quantile Plot),简称Q-Q图,是一种分析数据的图形化工具,常用于确定两组数据是否来自共同分布的总体。
这篇文章将从如下几个方面介绍Q-Q图:
①什么是分位数?
②如何绘制Q-Q图?
③什么是正态概率图?(一种特殊的、常用的Q-Q图。)
④正态概率图的参考线
⑤如何识别数据的偏态性
01 什么是分位数
Q-Q图是一组数据的分位数与另一组数据分位数的对比图。在Q-Q图中,「分位数」是一个重要概念。所以,我们先了解下什么是分位数?
分位数,是将概率分布的范围划分为概率相等的连续区间,或以相同方式划分样本中的观测点的值。常用的四分位、十分位和百分位。
1)四分位
假设现有9个数据,从小到大排列如下,现在求其四分位数。
1.1、3.2、4.1、6.5、9.8、10.9、13.2、15.3、16.4 (升序排列)
① 第一四分位数
a.先求秩
共有9个数据,第一四分位的秩为:(9 1)/4=2.25,说明第一四分位数位于第2个和第3个数据之间,也就是在3.2和4.1之间。
b.再求数
知道了第一四分位数的区间,但具体为多少呢?可以使用下面的方法求得:

可见,第一四分位分数是3.875。注意:这个数并不在数据集中。
② 第二四分位数(也就是:中位数)
同样,先求秩为:(9 1)*(2/4)=5。从数据集的开头往下数到第五个数据是9.8,所以第二四分位数是9.8。
③ 第三四分位数
先求秩:(9 1)*(3/4)=7.5,说明数据在第7个数据和第8个数据之间,按照下列方法可求得为:14.25。

2)十分位数
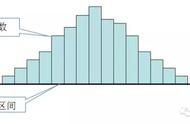
拿标准正态分布来举例。把标准正态分布分成10等分,计算出其Z值。如下图所示。

在标准正态分布中,左侧和右侧相对要矮而宽,而中间部分则是高而窄,但①-⑩区域的面积是一样的,概率是一样的,都等于0.1。所有区域累计起来的概率是1。
其中,第一个十分位数是-1.28,第二个十分位数是-0.84…第九个十分位数是1.28。
3)百分位数
这也是一种常用的方法,计算方法和四分位的计算类似。利用Minitab和Excel很容易求得。
02 如何绘制Q-Q图
Q-Q图由横轴(X轴)和纵轴(Y轴)组成,其中:
横轴(X轴): 第一组样本的数据
纵轴(Y轴):第二组样本的数据
Q-Q图中,不绘制实际的分位数,而是以各自数据为单位来绘制的。但,Q-Q图中的所有点对应的X轴和Y轴的数据,都具相同分位数。
判断两组样本数据是否来自相同总体的判据:所有点落在一条直线上(或非常靠近),那么可以认为两组数据具有相同的分布(来自同一总体)。
下面举例说明。
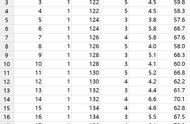
现在有三组数据。分别是:(以下四个样本都是25个数据)
①从服从标准正态分布N(0,1)的总体中抽取两组大小为25的样本数据,具体为下表蓝色和浅橙色所在列的数据。
②从服从正态分布N(5,3)的总体中抽取一组大小为25的样本数据,具体为下表灰色所在列的数据;
③从服从尺度为0.8,阈值为0的指数分布中抽取一组大小为25的样本数据,具体为下边浅绿色所在列的数据。