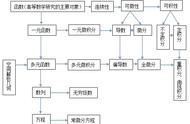
“微积分是近代数学中最伟大的成就,对它的重要性无论做怎样的估计都不会。” ——冯·诺伊曼
“在一切理论成就中,未必再有什么像17世纪下半叶微积分的发明那样被看作人类精神的最高胜利了!” ——恩格斯
十七世纪,函数的概念被提了出来,这为微积分的出现铺平了道路。同时,也是由于科学技术的发展,以及生产过程中对新的数学方法的迫切需要,一门新的数学分支——微积分,就继解析几何之后产生了。微积分是继欧几里得几何之后,数学界的一个最大的创造!
(一)千呼万唤始出来
微积分学是微分学和积分学的总称,在后面的具体内容中,我们将要对微分和积分的概念作出解释,这里先介绍一下这门学科创立的过程和它的基本思想。
从微积分成为一门学科来说,是在十七世纪,但是,微分和积分思想在古代就已经产生了。
拿积分的思想来说,公元前三世纪希腊的阿基米德(前287-前212)在研究解决抛物弓形的面积、球和球冠面积、螺线下面积和旋转双曲体的体积的问题中,就隐含着近代积分学的思想。
拿作为微积分学的基础的极限论来说,早在古代就已比较清楚的论述。比如我国的庄周(约前369-约前286)所着的《庄子》一书的“天下篇”中,记有“一尺之棰,日取其半,万世不竭。”三国时代的刘徽在他的割圆术中提到“割之弥细,所失弥小,割之又割,以至于不可割,则与圆周合体而无所失矣。”这些都是十分朴素的、也是很典型的极限概念。

图一 割圆术
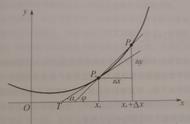
到了十七世纪,有许多科学问题需要解决,这些问题也就成了促使微积分产生的因素。归结起来,大约有四种主要类型的问题:第一类问题是研究运动的时候直接出现的,也就是要求出即时速度的问题。第二类问题是求曲线的切线的问题。第三类问题是求函数的最大值和最小值问题。第四类问题是求曲线长、曲线围成的面积、曲面围成的体积、物体的重心、一个体积相当大的物体作用于另一物体上的引力。
十七世纪的许多着名的数学家、天文学家、物理学家都为解决上述几类问题作了大量的研究工作,如法国的费尔马、笛卡儿、罗伯瓦(1602-1675)、笛沙格(1591-1661)、英国的巴罗、瓦里土(1616-1703)、德国的刻卜勒、意大利的卡瓦列利(1598-1647)等人都提出过许多很有建树的理论。为微积分的创立作出了贡献。
(二)两颗巨星的碰撞
要弄清楚微积分的创立过程,不得不到两个人。十七世纪下半叶,在前人工作的基础上,英国的牛顿和德园数学家菜布尼茨分别在自己的国度里研究和完成了微积分学的创立工作。虽然这只是十分初步的,但是,应该承认,他们各自独立地建立起微积分学的体系。他们的最大功绩是把两个貌似不相关的问题联系起来,一个是切线问题(微分学的中心问题),一个是求积问题(积分学的中心问题)。
牛顿研究微积分着重于从运动学来考虑,莱布尼茨却是侧重于从几何学来考虑的。

图二 牛顿
牛顿在1671年写了《流数法和无穷级数》,这本书直到1736年才出版,他在这本书里指出,变量是由点、线和面的连续运动产生的,否定了以前自己认为的变量是无穷小元素的静止的集合。他把连续变量叫做流动量,用U,x,y,Z,等表示。把这些流动量的导数叫做“流动率”,或者叫做流数,或叫做“速度”、“迅度”。他还使用了“刹那”(或译成“瞬”)这种名称。他在另一部着作《曲线求积论》中又重新解释了他新使用的符号。
牛顿在流数术中所提出的中心问题是第一已知连续运动的路径,求给定时刻的速度(也就是微分法);第二已知运动的速度求给定时间内经过的路程(也就是积分法)。
德国的莱布尼茨是一个博学多才的学者,1684年,他发表了现在世界上认为是最早的微积分文献,这篇文章仅有6页纸,内容并不丰富,标题很长而且很古怪,叫做“一种求极大极小和切线的新方法,它也适用于分式和无理量.以及这种新方法的奇妙类型的计算”。就是这样一篇说理也颇含混的文章,却有划时代的意义。它已含有现代的微分符号和基本微分法则。1686年,菜布尼茨发表了第一篇积分学。他是历史,上最大的符号学者之一。他所创设的微积分符号,远远优于牛顿符号,这对微积分有根大的影响。现在还在通用的符号如dx、dy,就是当时莱布尼茨精心选用的。

图三 莱布尼兹
(三)谁创立了微积分?
微积分学的创立,极大地推动了数学的发展,过去很多初等数学束手无策的问题,运用了微积分。往往就会迎刃而解,显示出微积分学非凡的威力。
前面已经提到,以门学科的创立绝不是某一个人的业绩,它必定是经过多少人的努力之后,在积累了大量成果的基础上,最后由某一个或几个人总结完成的。毫不例外,微积分学也是这样。
不幸的是,由于人们在欣赏微积分的宏伟功效之余,在提出谁是这门学科的创立者的时候,竟然引起了一场轩然大波,造成了欧洲大陆的数学家和英国数学家的长期对立。英国数学在一个时期里闭关锁国,囿于民族偏见,过于拘泥在牛顿的“流数术”中停步不前,因而数学发展整整落后了一百多年。
其实,他们是自己独立研究,在大体上相近的时间里先后完成的。比较特殊的是牛顿创立微积分要比莱布尼茨早10年,但是正式公开发表微积分这一理论,莱布尼茨却要比牛顿发表早三年。他们的研究都各有长处,也都各有短处。那时候,由于民族偏见,关于发明优先权的争论竟从1699年始延续了一百多年。
应该指出,这是和历史上任何一项重大理论的完成,也要经历一段时间一样,牛顿和菜布尼茨的工作也都是很不完善的。他们在什么是无穷小量这个问题上,其说不一,十分含煳。牛顿的“刹那”(“瞬”)或无穷小量,有时候是零,有时候不是零而是有限的小量;莱布尼茨的dx,dy也是不能自圆其说的。这些基础方面的缺陷,使得牛顿被神学家贝克莱(1685-1753)勐烈攻击,莱布尼茨被尼文太(1654-1718)竭力反对。

图四 伯努利
任何新兴的、具有无限前途的科学成就都吸引着广大的科学工作者,瑞士的雅科布·贝努利(1654-1705)和他的兄弟约翰·贝努利(1667-1748)、欧拉、法国的拉格朗日(1736-1813)等数学家都集中力量去解决牛顿和莱布尼茨遗留下来的问题,为微积分的发展作出了极为可贵的贡献。
,