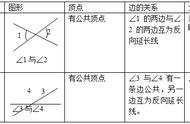
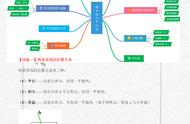
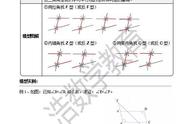
我们中学时所学习到的平面几何,可以说都属于欧式几何。其中平行线的定义包括三个基本特征:1.在同一平面内2.两条直线,3.不相交。
而关于直线的定义是,在二维平面上的两个点之间有且只有一条直线,也就是我们常说的两点确定一条直线。这些内容最早出现在《几何原本》里,由欧几里得编著。

那么平行线相交到底是怎么一回事呢?
这就要从两个人说起,罗巴切夫斯基和黎曼,罗巴切夫斯基是非欧几何的重要创始人,是他的质疑打破了人们对几何的认知,从此走出欧式几何,探索更广阔的数学世界,后人称他创造的数学门类为罗氏几何。

而黎曼则是另一个非欧几何中的重要代表,与以上两者不同却又不可分割,可以说是非欧几何的重要奠基人之一,后人称他创造的数学门类为黎曼几何。

欧式几何、罗氏几何、黎曼几何是三种相近却又不相同的几何。在各自的理论推论下都构成了一个严密的公理体系,虽然说都是正确的,但依靠的数学体系是不同的。而在每一种体系中各有一套理论,有个很好的例子,三角形的内角和为180度,这是我们从小要记的在平面讨论的情况,罗巴切夫斯基打破常规地认为三角形的内角和可能小于180度,而黎曼的学说则是证明了三角形的内角和可以大于180度。我们把三角形画在马鞍面和球面上就很好理解了,但这些都是曲边三角形,要想知道其中的定义和证明就要深入研究这两种学说了。

回到平行线的问题,类比刚刚的三角形,我们发现,在曲面上的两条直线,可能出现在平行的假设前提下相交或者相离的情况,甚至在一个球面上过两点可以作无数条直线。这显然不是我们用欧式几何思维能理解的。

那么你可能会觉得平行线相交肯定在现实中是不存在的,或者说是极为少见的,不过事实并不是这样。
爱因斯坦在相对论的基础上,构建了新的宇宙观,其中就指出了平坦的时空只不过是宇宙中小尺度上的特例,在大尺度的对比观察下,时空是弯曲不规则的,非欧几何可以说更贴合宇宙的实质。简单说就是整个宇宙其实是凹凸不平的,存在着很大的曲率,之所以我们观察得出的宇宙近乎平整,但也只能说明我们观察的尺度较小,从整个宇宙的尺度上来说,是不存在绝对的平行线,无限延长的两条线会因为宇宙的曲率相交或者发散,所以平行线相交很多时候是普遍存在的。
就好比在研究地球时,例如航船航空这些路径,就不是简单的欧式几何,我们所讲的直线在地球这个整体看来有很大的弧度,这都归结于球体的曲率。

总的来说,平行线能不能相交取决于它放在哪种数学体系中,而不是简单的直觉判断。
,