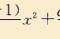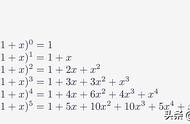今天我们来介绍一下二项式定理,二项式定理是研究类似
这种表达式如何展开的问题。我们都知道:
如果2换为n,且n>0,那么这样的表达式,该如何展开呢?其实这是个排列组合问题,依照排列组合知识,表达式,其通用展开公式是:
这个公式很长,但是其实是有规律的,那就是每一项可以表示成如下通用的公式:
这个通用的公式,就是表示展开后每项的通用表达,展开后有n 1项,把项数r代入上述通用公式,就能得出该第r项的表达式。这个通用表达式,本身也是很有规律的,那就是组合的上标数跟后面的的指数一样,而a的指数对应就是n-r,也就意味着第一项a的指数 第二项b的指数,一定等于n,即:。
利用这个通用公式特征,我们可以很快的求出一个具体二项式的某项的指数的系数。举例:
,求项的系数是多少。
解答:
把,先看一下,这两项相乘,如何才能凑成项呢?很简单,我们先第一部分出,第二部分出(注意,第一部分的指数 第二部分的指数,要等于5),两者相乘正好凑成,按通用项公式,r=4,代入公式得:
所以,,项的系数是10。