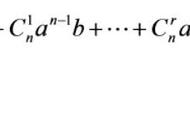说到二项式定理,这应该是初等数学中比较有趣的一个内容。因为二项式定理涉及到了代数学,组合学。很多的关于二项式定理的文章都是讲如何通过组合方法或者数学归纳法来证明二项式定理的。组合论证方法以及数学归纳法都是初等数学中的经典内容,组合论证二项式定理的证明过程看上去有些抽象,而数学归纳看起来更像是事先知道结果而进行的略有些枯燥的论证。这里并不是说这两种方法不好,只是说这两种方法看上去更像是某种灵光乍现的猜想。这两种具有猜的性质的方法证明了二项式定理。

数学的历史上很多优秀的结果以及进展都是通过猜想的方法得到的,牛顿也是通过猜想的方法得到广义二项式定理的,而广义二项式定理的证明是由欧拉完成的。猜想是推动数学进步的重要手段,著名数学家波利亚也是这样认为的。
众所周知的费马猜想作为难倒数学家百年的难题被怀尔斯证明了,而费马猜想对于数学的贡献不仅仅是其证明本身,而是在于数学家们不断的探索证明方法的过程中所提出的新方法,新思想。

数学家怀尔斯
各种各样的数学猜想在挑战人类智慧的同时也推动着人类数学文明的发展。
可以确定的是:猜想是数学中非常重要的方法! 但是如果让学生更好地掌握二项式定理,作为学生有时会希望通过更直观地方法记忆二项式定理,这时通过高等数学的方法进行二项式定理的验证可以给人一定的启发。有一本非常著名的数学著作叫做《高观点下的初等数学》里面的内容就是数学家克莱因用高等数学的观点去审视初等数学,读者可以发现很多初等数学中比较困难的问题通过高等数学工具的引入都能得到很简单验证。我们可以用导数法来验证二项式定理,可以帮助我们更好地记忆二项式定理。
我们用导数法来验证二项式定理可以让我们看到高等数学与初等数学的一些联系,但是这种验证并不能称为证明,这是因为验证所用到的结论是由二项式定理证明而来的。
要验证二项式定理我们会进行如下思考:
我们想把如下的式子展开成指数次幂相加的形式,那么我们应该怎么做?

我们不妨假设1 x的n次方可以展开成如上图所示右边的形式,在这个等式的右边:a1,a2,a3...这些都是待定的系数。
我们对f(x)求一次导可得到如下图所示的形式:

观察常数项a1,当我们去x=0时,可以得到a1的表达式:

我们继续对f(x)求二次导,三次导并带入x=0可得:

这样我们就验证了二项式定理。
二项式定理是数学中非常基本的定理之一,用高等数学的方法验证出二项式定理的过程看上去非常简单。
用导数法来验证二项式定理是高等数学在初等数学中的一个应用,如果严格证明二项式定理的话可以用数学归纳法和组合论证方法,比较组合论证法与数学归纳法,你认为哪种方法更有趣呢?你认为还有什么方法可以证明二项式定理呢?谈谈你的看法!
,