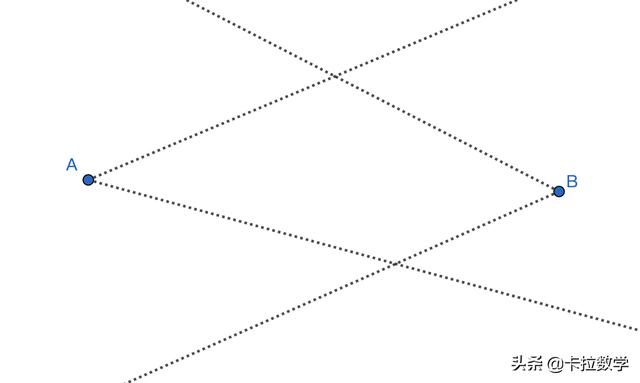
题目:纸上两点A和B,它们之间的距离大于直尺的长度。你如何只用直尺作出过这两点的连线?注意,你只能使用笔和直尺,不能借助圆规等其它工具。

你是不是从来没有想过自己会遇到直尺不够长的尴尬情况,作为数学天才的你,难道要再买一把更长的直尺吗?
如果你想思考一下,可以暂停滚屏,思考1分钟后,再继续。
思路:
方法是来自于非常有趣的射影几何学,其中大名鼎鼎的笛沙格定理(Desargues)。
我们先简单介绍一下这个定理:
笛沙格定理:平面上有两个三角形△ABC、△DEF,设它们的对应顶点(A和D、B和E、C和F)的连线交于一点,这时如果对应边或其延长线相交,则这三个交点共线。其逆定理也成立。
转化为白话文:若两个三角形对应顶点的连线共点,则对应边的交点共线。

百度上可以找到很多这个定理的证明方法,有兴趣的读者可以自行查阅。
准备工作完成,我们开始啦!
第一步:
从A点出发,向任意两个方向作射线。两条射线的夹角应该尽可能小,因为一会儿要连接射线上的两点,太远了当心直尺够不着。对B点作相同的处理。
第二步:
画出这两对射线的交点M和N。连接并延长MN,在MN上任意找一点X。

第三步:
从点X出发,向任意两个方向作射线(这两条射线的夹角也是越小越好,原因同上),其中一条射线与从A出发的两条射线交于P1,Q1,另外一条射线与以B为端点的两条射线交于P2,Q2。

注意,△NP1P2和△MQ1Q2两个三角形构成了一个满足笛沙格定理的图形,因此P1P2和Q1Q2的交点必然与点A、点B共线。

此时,我们就找到了所求直线上的一个新的点C。
第四步:
接下来,我们只需要将C点和已有的A或者B相连,并且延长直到贯穿A、B两点。
大功告成!你get到这个技能了吗?
还有未解决的意外情况:
但是事情貌似没有结束,还有疑点。这么做的前提是C的位置离A和B中的某个点足够近才行。要是C点离A和B仍然很远咋办?
起初M和N的距离,P1和P2的距离,以及Q1和Q2的距离,我们都是可以控制的,这可以保证我们的直尺够得着;但鬼知道这样作出来的C点跑哪儿去了呢?这怎么办呢?多试几次直到作出一个合适的C来?
其实解决办法很简单,稍微调整一下射线X-P1-Q1的角度,我们又能作出一个新的点C’,显然C和C’的距离可以达到任意小,并且C和C’两点都在AB上。连接C和C’后,我们就可以无限延长直线AB了。
现在你可以自信地把长直尺换成短直尺。嘿嘿
你做对了吗?如果你有更好的方法,欢迎分享。
【卡拉数学】长期分享数学趣题、解题技巧,致力于数学科普和拓展数学思维,每日定更,觉得内容有兴趣的可以长期关注哦!