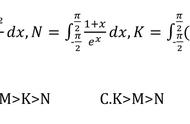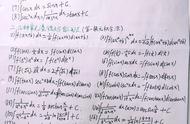所以我们就证明完了,整个证明过程并不难,比较困难的点在于我们在处理等式右边的时候是怎么想到令Φ(t) = F(φ(t))的呢?这是一个非常巧妙的点。想到这个不太容易,如果是我从头开始证明,我可能会往Φ(t)的原函数上想,估计不太容易想到将F(x)引入进来。
我们理解了换元求解定积分的方法之后,我们一起来看一道例题来熟悉一下。这个例题还是经典的三角换元:

我们很容易想到我们可以令x = a sint,这样的话 dx = a cost dt。当x=0时,t=0,当x=a时,t= π/2,我们代入原式可以得到:

明白了原理之后,我们也可以将换元公式反过来用。也就是说当我们凑到 t = φ(x) 的情况时,也一样可以使用换元公式。
我们再来看一个例子:

我们很容易凑到 t = cosx时,dt = -sinx dx,当x=0时,t=1, 当x=π/2时,t=0。我们代入原式,可以得到: