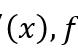编辑切换为居中
添加图片注释,不超过 140 字(可选)
例2 求方程y¢¢ 2y¢ y=0满足初始条件y|x=0=4、y¢| x=0=-2的特解.
解 所给方程的特征方程为
r2 2r 1=0, 即(r 1)2=0.
其根r1=r2=-1是两个相等的实根, 因此所给微分方程的通解为
y=(C1 C2x)e-x.
将条件y|x=0=4代入通解, 得C1=4, 从而
y=(4 C2x)e-x.
将上式对x求导, 得
y¢=(C2-4-C2x)e-x.
再把条件y¢|x=0=-2代入上式, 得C2=2. 于是所求特解为
x=(4 2x)e-x.
例 3 求微分方程y¢¢-2y¢ 5y= 0的通解.
解 所给方程的特征方程为
r2-2r 5=0.
特征方程的根为r1=1 2i, r2=1-2i, 是一对共轭复根,
因此所求通解为
y=ex(C1cos2x C2sin2x).
n 阶常系数齐次线性微分方程: 方程
y(n) p1y(n-1) p2 y(n-2) × × × pn-1y¢ pny=0,
称为n 阶常系数齐次线性微分方程, 其中 p1, p2 , × × × , pn-1, pn都是常数.
二阶常系数齐次线性微分方程所用的方法以及方程的通解形式, 可推广到n 阶常系数齐次线性微分方程上去.
引入微分算子D, 及微分算子的n次多项式:
L(D)=Dn p1Dn-1 p2 Dn-2 × × × pn-1D pn,
则n阶常系数齐次线性微分方程可记作
(Dn p1Dn-1 p2 Dn-2 × × × pn-1D pn)y=0或L(D)y=0.
注: D叫做微分算子D0y=y, Dy=y¢, D2y=y¢¢, D3y=y¢¢¢, × × ×,Dny=y(n).
分析: 令y=erx, 则
L(D)y=L(D)erx=(rn p1rn-1 p2 rn-2 × × × pn-1r pn)erx=L(r)erx.
因此如果r是多项式L(r)的根, 则y=erx是微分方程L(D)y=0的解.
n 阶常系数齐次线性微分方程的特征方程:
L(r)=rn p1rn-1 p2 rn-2 × × × pn-1r pn=0
称为微分方程L(D)y=0的特征方程.
特征方程的根与通解中项的对应:
单实根r 对应于一项: Cerx ;
一对单复根r1, 2=a ±ib 对应于两项: eax(C1cosbx C2sinbx);
k重实根r对应于k项: erx(C1 C2x × × × Ck xk-1);
一对k 重复根r1, 2=a ±ib 对应于2k项:
eax[(C1 C2x × × × Ck xk-1)cosbx ( D1 D2x × × × Dk xk-1)sinbx].
例4 求方程y(4)-2y¢¢¢ 5y¢¢=0 的通解.
解 这里的特征方程为
r4-2r3 5r2=0, 即r2(r2-2r 5)=0,
它的根是r1=r2=0和r3, 4=1±2i.
因此所给微分方程的通解为
y=C1 C2x ex(C3cos2x C4sin2x).

编辑切换为居中
添加图片注释,不超过 140 字(可选)
二、二阶常系数非齐次线性微分方程简介
二阶常系数非齐次线性微分方程: 方程
y¢¢ py¢ qy=f(x)
称为二阶常系数非齐次线性微分方程, 其中p、q是常数.
二阶常系数非齐次线性微分方程的通解是对应的齐次方程
的通解y=Y(x)与非齐次方程本身的一个特解y=y*(x)之和:
y=Y(x) y*(x).
当f(x)为两种特殊形式时, 方程的特解的求法:
一、 f(x)=Pm(x)elx 型
当f(x)=Pm(x)elx时, 可以猜想, 方程的特解也应具有这种形式. 因此, 设特解形式为y*=Q(x)elx, 将其代入方程, 得等式
Q¢¢(x) (2l p)Q¢(x) (l2 pl q)Q(x)=Pm(x).
(1)如果l不是特征方程r2 pr q=0 的根, 则l2 pl q¹0. 要使上式成立, Q(x)应设为m 次多项式:
Qm(x)=b0xm b1xm-1 × × × bm-1x bm ,
通过比较等式两边同次项系数, 可确定b0, b1, × × × , bm, 并得所求特解
y*=Qm(x)elx.
(2)如果l是特征方程 r2 pr q=0 的单根, 则l2 pl q=0, 但2l p¹0, 要使等式
Q¢¢(x) (2l p)Q¢(x) (l2 pl q)Q(x)=Pm(x).
成立, Q(x)应设为m 1 次多项式:
Q(x)=xQm(x),
Qm(x)=b0xm b1xm-1 × × × bm-1x bm ,
通过比较等式两边同次项系数, 可确定b0, b1, × × × , bm, 并得所求特解
y*=xQm(x)elx.
(3)如果l是特征方程 r2 pr q=0的二重根, 则l2 pl q=0, 2l p=0, 要使等式
Q¢¢(x) (2l p)Q¢(x) (l2 pl q)Q(x)=Pm(x).
成立, Q(x)应设为m 2次多项式:
Q(x)=x2Qm(x),
Qm(x)=b0xm b1xm-1 × × × bm-1x bm ,
通过比较等式两边同次项系数, 可确定b0, b1, × × × , bm , 并得所求特解
y*=x2Qm(x)elx.
综上所述, 我们有如下结论: 如果f(x)=Pm(x)elx, 则二阶常系数非齐次线性微分方程y¢¢ py¢ qy =f(x)有形如
y*=xk Qm(x)elx
的特解, 其中Qm(x)是与Pm(x)同次的多项式, 而k 按l不是特征方程的根、是特征方程的单根或是特征方程的的重根依次取为0、1或2.
例1 求微分方程y¢¢-2y¢-3y=3x 1的一个特解.
解 这是二阶常系数非齐次线性微分方程, 且函数f(x)是Pm(x)elx型(其中Pm(x)=3x 1, l=0).
与所给方程对应的齐次方程为
y¢¢-2y¢-3y=0,
它的特征方程为
r2-2r-3=0.
由于这里l=0不是特征方程的根, 所以应设特解为
y*=b0x b1.
把它代入所给方程, 得
-3b0x-2b0-3b1=3x 1,

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)
提示:
y*=x(b0x b1)e2x=(b0x2 b1x)e2x,
[(b0x2 b1x)e2x]¢=[(2b0x b1) (b0x2 b1x)×2]e2x,
[(b0x2 b1x)e2x]¢¢=[2b0 2(2b0x b1)×2 (b0x2 b1x)×22]e2x.
y*¢¢-5y*¢ 6y*=[(b0x2 b1x)e2x]¢¢-5[(b0x2 b1x)e2x]¢ 6[(b0x2 b1x)e2x]
=[2b0 2(2b0x b1)×2 (b0x2 b1x)×22]e2x-5[(2b0x b1) (b0x2 b1x)×2]e2x 6(b0x2 b1x)e2x
=[2b0 4(2b0x b1)-5(2b0x b1)]e2x=[-2b0x 2b0-b1]e2x.
方程y¢¢ py¢ qy=elx[Pl (x)coswx Pn(x)sinwx]的特解形式
应用欧拉公式可得