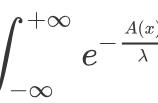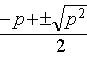用拉氏变换法求解线性定常微分方程的过程归纳如下:
1, 考虑初始条件,对微分方程中的每一项分别进行拉氏变换,将微分方程转换为变量s的代数方程;
2, 由代数方程求出输出量拉氏变换函数的表达式;
3, 对输出量拉氏变换函数求反变换,得到输出量的时域表达式,即为所求微分方程解。
微分方程解的运动模态:
线性微分方程的解由特解和齐次微分方程的通解组成,通解由微分方程特征根所决定,称为瞬态分量,表示解随时间瞬时变化过程,也称为自由运动,特征根的类型和特征根的重根数对自由运动的形态产生不同的影响,单重实数根的运动模态是按指数规律衰减的瞬态分量;单重复数共轭根的运动模态是按指数规律衰减的震荡瞬态分量;多重根的运动模态不仅按指数规律衰减,而且还与时间乘积有关。
对于一般的微分方程式,拉氏变换反变换的求解方程总结为:
令拉氏代数方程的特征根为:

则求解拉氏反变换:

工程中,通常定义β=180-θ,则上式也可以写为