直升机前进的动力来自哪,直升机前进的推力是从哪里来的

作者：丁尹

不负责任的声明：本文是一篇偏学术派的硬核专业笔记，如因强行阅读本文诱发头晕目眩、昏昏欲睡等症状，丁某概不负责。

※ 受限于头条编辑器的限制，本文用LaTex语言写的公式无法显示，如有阅读公式的需求，还请读者朋友自行搜索网络LaTex公式转码工具查看，谢谢。

正经来说，本文本来确实是一份笔记稿，不过成稿已经有一些时间了，最近在回顾高前进比旋翼[注1]相关内容，顺手整理出来与大家交流。主要记录了两个部分的内容，第一个部分阐述了一种关于叶素段如何对应360°翼型气动系数C81表的小技巧，这个小技巧对于刚开始进行旋翼气动分析或者从低阶气动模型逐渐转向高阶气动模型的读者朋友也许有一定的参考价值；第二部分内容对高速直升机旋翼在高前进比状态下桨叶诱导的一些涡运动的特性，其中涉及两篇参考文献，如果没有做过高速直升机旋翼气动方面的研究而想要较好地理解这部分内容的话，建议还是先大致略读以下这两篇参考文献最佳。

作为一篇笔记稿，本文更多的是一些我自己在进行一些问题的探究过程中的思考，所以其置信度低于通过同行评议的学术论文，大致上与预印本相当，望有深度阅读需求的读者朋友知悉。

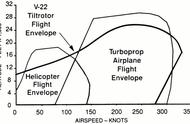
[注1] 所谓前进比即是mu = Vf/Vtip，其中mu就是前进比，Vf是指飞行器的飞行速度，而Vtip是指旋翼的桨尖线速度，对于常规直升机来说，其前进比的极限值一般决不可能超过0.4。高前进比就是指的mu值比较高的情况，对于到底多高能被称为高前进比状态，不同的研究人员有不同的说法，不过mu = 0.6（Graham Bowen-Davies；2018）是一个认可度比较高的前进比边界，本文同样认为0.6以下为低前进比，以上则为高前进比状态。

在旋翼的气动分析中，翼型的升阻力特性获取可谓是相当重要的一环，准确的翼型升阻力特性可以提高计算结果的置信度和精度，而不准确的翼型升阻力特性则可能导致配平发散甚至得到错误的结果，在高速高前进比的状态下，气流的强不对称性愈发明显，旋翼气动环境更为复杂，要对旋翼气动特性进行准确计算，首当其冲的就是获取准确的叶素升阻力系数。

为了准确获得叶素升阻力系数，最常用的方法就是先获取对应翼型的360°吹风数据，然后通过插值的方式来得到所需要的结果。但是在代码编写的过程中，我发现常规的叶素气动力系数插值方法，常常存在针对某种来流状态或某种独特翼型的简化假设，导致这些方法无法用于流动复杂、迎角变化幅度大的高前进比状况，为了解决这一问题，我采取了一种全矢量求解迎角和气动力方向的计算策略。

在风洞实验中，常规的做法是保持来流不变，以翼型前缘正对来流为零度迎角，绕气动中心抬头旋转，将翼型从前缘至后缘连成一条矢量线，该矢量与来流方向的夹角就是翼型与来流的迎角 α ，每隔一个给定的角度变化小量，记录一次稳态的升阻力系数，最后统计成表就是常见的翼型升阻力系数C81表。

在这种试验方式下，阻力的正方向很容易确定，因为阻力矢量与来流矢量始终保持一致，这是毋庸置疑的，而升力的正方向则由以下公式

$$\vec{V}_a \times \vec\alpha$$

来决定，其中 va 表示来流速度矢量，α 表示迎角方向矢量（由零升迎角和右手法则确定），其物理意义实则可以是从茹科夫斯基升力定律中来的：

$$T = \rho_a \vec{v}_a \times \Gamma$$

$$\Gamma = \oint \vec{v} ds$$

上式中，Γ为绕翼型环量，通过它的计算公式可以看出，环量方向实则与翼型表面速度流动方向一致，由伯努利定律，风洞中产生正升力的翼型上表面流动要大于下表面，因而Γ的方向实则与迎角转动的方向一致，由此便可以得到升力的正方向，而在风洞实验中，这个方向一般取为竖直向上。

在实际的旋翼叶素气动力计算中，来流的方向不像风洞那样是保持不变的，旋翼的角度也不是某一个确定的静态值。处于飞行来流、旋转来流、诱导来流等多重流动作用中的叶素，其气动迎角和升阻力方向的确定远比风洞要复杂。但是，为了计算方便，在常规直升机的叶素气动力计算中，迎角（如下图所示）一般由安装角 θ 与来流角φ 之差给出，式中uT , uP 分别为切向（周向）来流和轴向来流。

$$ \alpha = \theta - \phi $$

$$\phi = tan^{-1} \frac{u_p}{u_T}$$

▲叶素来流迎角和升阻力方向示意图

对于常规直升机而言，除靠近桨根的少部分桨叶段之外（这部分叶素气动力在常规旋翼计算中往往会进行简化处理），绝大部分叶素周向来流都远大于诱导速度，总体而言气动迎角都会落在-15~20°区间，也就是说在大部分状况下，升力系数与迎角是线性关系，升力的方向也比较容易确定，因而这样的简化求解方式是合理的；但是对于高前进比旋翼而言，反流区较大，后行侧大部分桨叶都将进入反流区，周向来流都是从后缘吹向前缘，而反流区内，靠近桨尖的大部分区域，轴向诱导速度相比周向来流，其量级不再有显著差异，因而在旋翼周期运动中，其叶素来流迎角变化幅度将会较为巨大，这种情况下，常规的迎角计算方法将不再适用，比如下图所示的状况。

▲翼型后缘来流示意图

观察上图，从直观可以判断出其气动迎角应当是落在180°附近的区域，但是直接用安装角与来流角之差难以计算准确迎角，而且其升力方向与风洞升力系数之间的关系也并不明显，无法用常规方法中的某一解析公式来进行计算。

针对上述问题，一种解决方案是采用分段迎角求解方法，考虑来流的不同方向，将迎角计算域分为多个区域（如分为四个——前缘上方、前缘下方、后缘上方、后缘下方），以此来计算正确的迎角和升阻力系数。这种方法针对特定的翼型能取得较好的效果，实则上却存在通用性的问题，不同的翼型将要选择不同的分段方式，比如说，对于存在零升迎角的非对称翼型，其分段区域的划分显然与对称翼型不同，而在高前进比旋翼的外形优化设计中，将应用多种翼型分段布置，如果用这种分段方式，其通用性和效率都不佳，也不利于研究工作的进一步展开。

为解决上述问题，采用了一种全矢量求解的策略来处理迎角求解和升阻力方向计算的问题，经验证，该方法能做到将实际情况与风洞数据一一对应起来，通用性较好。