直升机前进的动力来自哪,直升机前进的推力是从哪里来的

▲惯性坐标系组示意图

该方法的基本思路是，首先建立一整套惯性坐标系组（如上图所示），包括桨毂坐标系（下标hub），桨叶旋转坐标系（下标ro），桨叶挥舞坐标系（下标β），叶素当地坐标系（下标be，翼型气动中心为原点，前缘指向后缘为正方向），并计算各坐标系之间的转换矩阵，将速度、控制点等量都作为矢量的形式表示在各个坐标系中，而最后在求解旋翼迎角的时候，将叶素来流从其他坐标系中转换到叶素当地坐标系中，并且表示为矢量的形式，通过计算其与叶素翼型前缘到后缘连线这一矢量之间的夹角来确定准确的来流迎角（为服务于矢量计算，保证角度变化的连续性，本方法中迎角取0°到360°，而非传统的-180°到180°[注2]），在这种坐标系下，升力的矢量方向将由下述方式确定

# 迎角的确定 v_be = rotobe(v_air, β, θ) # 将来流速度矢量转化到叶素坐标系下 v_be_2d = [v_be[2],v_be[3]] # 在叶素坐标系下，得出速度在叶素剖面二维矢量 α = aoaget(v_be_2d) # 来流矢量与翼型前后缘连线矢量夹角即为实际气动迎角（0-360°） cl,cd = clcdget(α) # 升力方向的确定 if fcl(α) >= 0.0# 判断升力系数方向 lbe = [0, cos(α π/2), sin(α π/2)] # 若为正，则升力方向为迎角正转90°方向 else lbe = [0, cos(α-π/2), sin(α-π/2)] # 若为负，则升力方向为迎角逆转90°方向 end

上述代码中，fcl 为升力系数插值函数，fcl(α) 得到的就是对应迎角的升力系数值，lbe 表示升力正方向的矢量，通过该方式，实际升力的方向能自动与风洞数据匹配，因而可采用下述计算公式计算叶素微段单位升力矢量

$$L_e = \vec{lbe} \times |0.5 \rho v^2_r c \times fcl(\alpha)|$$

式中，Le 为叶素微段单位升力，vr 为叶素微段总的来流速度，c为弦长。

采用上述策略，不仅保证了迎角计算的准确性，同时保证了叶素升阻力系数的插值与风洞数据一一对应起来，且具有良好的通用性，能应用到任意翼型的数据插值中。

[注2] 在我以前的代码中（Fortran），0~360°方位角变化对于矢量求解代码编写比较友好，在我现在的代码（Julia）中，不管是按照0~360°还是-180~180°来求解，代码编写都一样简单，哈哈，推荐一波Julia语言（虽然这本质上其实不是代码语法的作用，主要是对问题的理解更深入了）

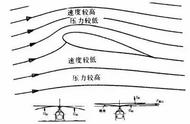
在常规直升机旋翼计算中，由于旋翼反流区较小，在工程计算中往往直接被忽略，而在高前进比计算中（如下图所示），反流区扩散到整个后行侧，旋翼有一半的时间在其中转动，处于其中的旋翼将不产生升力或者产生负升力，这种超常规的流动特性对旋翼的气动载荷和旋翼配平都产生了直接的影响，须谨慎考虑和处理。

▲旋翼前进比增大，反流区逐渐扩大示意图

在高前进比旋翼流场复杂物理现象中，其中最具有代表性的就是反流区中来流自尖锐后缘吹向前缘时，在后缘背风处形成的强涡结构以及由于前飞高速来流导致的桨叶径向强偏流效应（Yawed Flow)。强后缘分离涡生成之后，受到高速来流以及径向偏流的影响，与桨叶一起快速移动，导致大部分后行侧桨叶段都受到其影响，而受其影响的叶素微段气动力特性与常规状态下显然存在种种差异。就目前而言，这方面的相关研究尚且较少，方法体系尚不完善。基于从物理现象本身出发进行探索的考虑，本文采用了基于格子-玻尔兹曼（Lattice Boltzmann Method, LBM）的CFD方法进行流场可视化，以此对高前进比旋翼叶素的超常规物理特性进行了一些研究。

观察旋翼高速高前进比三维流场，可以看到大约在220°方位角的时刻，受高前进比来流的影响，后行侧桨叶的尾随涡无法再卷起为集中的桨尖涡，而靠近桨根的叶素微段处，来流从后缘吹向前缘，生成尖锐后缘涡（Sharp Edge Vortex, SEV），此时受到较强的朝向桨根的径向偏流影响，但是前期后缘涡黏着在后缘表面，拉伸效应不显著；而随着桨叶装过270°，后缘涡又受到较强的朝向桨尖的径向偏流影响，此时后缘涡已经不再是黏附状态，所以拉伸效应显著，加速了后缘涡的扩散。

▲涡量云图（观察点为桨盘下方）

▲桨盘下方平面内涡量演化图

从涡量演化图中还可以发现，高速来流中桨叶柄的后缘拖出了较强的集中涡，这也从一个方面解释了高前进比旋翼气动性能理论计算中桨盘后向力（阻力）比试验数据要小的现象，高速来流中的桨叶柄显然产生了较强的后向阻力，因而在高前进比气动分析中计入这个现象将提升计算的置信度，此外，该现象的出现也要求我们在进行高前进比旋翼优化设计的过程中，桨叶柄的优化设计也要纳入考量。