4素数寻找算法
素数行踪不定,分布未知,怎么样才能找到素数?
在公元前2世纪希腊数学家埃拉托斯特尼(Eratosthenes),就已经提出了一个非常简单而且有效的素数筛法,我们称之为埃拉托斯特尼筛法(Sieve of Eratosthenes)。核心是:要得到自然数n以内的全部素数,必须把不大于根号n的所有素数的倍数剔除,剩下的就是素数。
具体的筛法如下:
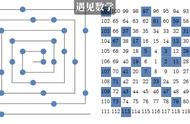
第1步:确定需要筛选素数的范围,确定范围的最大值,比如是120。
第2步:根号120的结果为10.95,所以只需要利用11以内所有素数的倍数来剔除120以内的数字,剩下的就是素数。首先剔除以2为倍数的数字,11以内剔除掉4,6,8,10这几个数字,同时剔除掉120以内所有以2为倍数的数字。
第3步:最小的未被剔除的数字为3,剔除以3为倍数的数字,11以内剔除9这个数字,同时剔除掉120以内所有以3为倍数的数字。
第4步:最小的未被剔除的数字为5,剔除以5为倍数的数字,11以内不需要剔除数字,同时剔除掉120以内所有以5为倍数的数字。
……
如此类推,可以将120以内的所有素数完全找到。

一个埃拉托斯特尼筛法的例子
5素数有什么用
为什么科学家们这么热衷于寻找素数?一方面,是对于自身理想的追求,孜孜不倦地在数学的高峰上攀登。但另一方面,素数在实际场景当中却体现很大的价值。
1、计算机领域
素数在计算机领域当中的应用,莫过于信息的加密,其中有著名的RSA算法(小智以前写过RSA算法的介绍,点击传送门)。由于目前大整数的因式分解,即寻找一个大整数的素数因子,是一件非常困难的事情。目前,除了暴力破解,还没有发现别的有效方法。也就是说,只要密钥长度足够长,寻找素数因子的时间则非常长,用RSA加密的信息实际上是不能被解破的。因此,素数在密码学当中有重要的地位。

只有拥有钥匙(私钥)的情况下,才能解出信息
2、工业领域
在汽车变速箱齿轮的设计上,相邻的两个大小齿轮齿数可以设计成素数,以增加两齿轮内两个相同的齿相遇啮合次数的最小公倍数,可增强齿轮的耐用度,减少故障。

汽车序列式变速箱的细节图
3、生物领域
北美的周期蝉(Magicicada)有着奇特的生命周期。它们要经过一段漫长的时间,每13或17年,才会成群地破土而出。
自17世纪中叶起,科学家就一直对周期蝉的生命周期困惑不已。它们遵循着相同的基本生命周期:幼虫在地底生活13或17年,然后在夏季大量出现。它们爬上树,蜕皮,成长为成虫,然后在短短数周内,成虫相遇、交配、产卵。孵化后,幼虫会回到地底,等待下一个轮回。
为什么是13或者17年,而不是其他数字,而恰好这个数字是素数?
当这些周期蝉大量出土繁殖时,周期蝉的天敌大吃特吃,天敌有更多的营养进行繁殖,天敌数量将会大大增加。假设天敌是6年才能性成熟,它的后代又要6年之后才会性成熟繁殖,因为没有周期蝉吃,它们的数量一直是回落的。再假设周期蝉的周期是18年,那么天敌们将在第18年继续大吃特吃,在这个18年周期内产生了更多的天敌,这样每过18年,天敌的总数不断上涨,周期蝉的数量就越来越少了。同理,周期是16年的周期蝉,很可能会被周期为2、4、8年的天敌吃到绝种。
而13年蝉和17年蝉刚好避过了这些可能性,因为13和17是素数,除非天敌每年繁殖,或者刚好13或17年繁殖,否则不可能成为帮助天敌进行繁殖。因为13年蝉和17年蝉选择了素数的生命周期,大幅度降低了帮助天敌繁殖的机会,使得自己能够生存到今天。