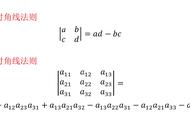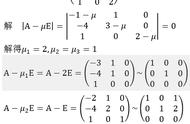由于对称的缘故,其各行相加之和相同,利用这一特性,将下面所有行都加到第一行上,并将公因子提出,如图所示。然后234列分别减去第一列,就会得到第四种类型的代数余子式型,然后进行降阶计算。
(六)重复,渐变式行列式
其特点是各行元素逐级递增或递减,有许多相同的元素也可以这样做,我们通常会从最后一行开始逐行往上相减,比如第四行减去第三行,第三行减去第二行...举例如下

这个例子比较特殊,不仅用这个方法可以解决利用性质五同样可以化简
(七)分块行列式
这类形式非常明显,0的位置十分集中,这就提醒我们利用拉普拉斯定理进行分块计算,例如
所以我们任取两行(令其为前两行)所得到的非零子式有M1=
其代数余子式为(-1)1 1 2 2
,相乘求出结果即可。

公式粘贴不上来,对不起了,看一下原文档的截图吧
(八)对角线变式型行列式
这一种主要是关于对角线对称,有两种解法。一种是进行逐行加减,和六的思路差不多,只不过后面的处理方法不大相同。另一种需要更严格的对称,可以用递推的方法做,我们留到二里讲。采用逐行相减的策略就能化为下面的形式,而后利用实际含义或者爪形行列式的运算法则就可以得出答案。
=