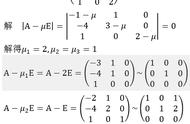作者 | P.A.M.Dirac
【摘要】本文描述了数学的完美性及其在粒子物理学中的重要性。
我在物理学中研究工作的主要部分不是着跟于解决某个特殊问题,而是单纯地考虑物理学家使用并试图以一种有趣的方式拟合在一起的那些数学量,不管这种研究能否得到应用。先单纯寻找数学的完美性。这个研究的应用可以放在以后完成。到那时,人们才会大获裨益。
我来给出上述过程的一个生动的例证。在1927年,有一次我曾用3个2×2矩阵做游戏,我 把这三个矩阵称为,,.这些矩阵每个的平方等于单位矩阵,并且它们之间互相反对易。我注意到,如果把它们分别与动量的三个分量相乘后相加,得出,这个量的平方正好等于.这是一个激动人心的结果.然而人们能用它做些什么呢?
我们把作为薛定谔波动方程中的哈密顿量,给出的波函数有两个分量,以便能把矩阵作用在它上面。于是我们得到一个相对论波动方程。然而这个方程只能用于静质量为零的粒子。为了得到静质量不为零的粒子的理论,我们需要四个互相反对易的矩阵,但这样的矩阵并不存在。所以这个研究结果不适用于我最感兴趣的电子。因此我不得不抛弃它。
过了几星期后我才认识到,没有必要把自己限于2×2矩阵,进而我用4×4矩阵使问题容易地得到解决。回顾那时人们竟如此不接受这样一个基本观点似乎是奇怪的。
所得到的波动方程对电子证明是非常成功的。它导致了电子自旋和磁矩的正确数值。这是完全出乎预料之外的。然而这些结果完全来自美妙的数学研究,当时并没有对电子给出这些物理结果的丝毫打算。
数学完美性的另一个例子是导致了磁单极子的概念。我做这个研究工作是希望对精细结构常数得到某种解释、然而这个希望没有成功。数学却无可辩驳地导致了磁单极子。
由于数学的完美性,按照理论的观点人们可以认为磁单极子应当存在。人们为寻找磁单极子做了许多尝试,然而都没有成功。人们将会得出这样一个结论:对自然界建立一个理论时数学本身的完美性不是一个充足的理由。在探索自然界的基本原理方面我们仍然要更多地学习。
我还希望讨论我在1970年由粒子的相对论理论推动的关于数学完美性的发展。在那里只用一个分量的波函数代替通常四个分量的波函数。而粒子具有由两个谐振子组成的固有自由度。把这些振子的坐标称为,其共辅动量称为,这四个满足如下的对易关系(取),
其中,是矩阵
注意,是斜对称矩阵,并且.
现在,我们把四个看作一个列矩阵,并用表示它。我们建立下面的波动方程
其中是4×4矩阵,它的平方等于单位矩阵.这些矩阵互相反对易并且与矩阵反对易.还必须把矩阵的元素选为实数,这个波动方程在形式上与通常电子的波动方程非常相似,差别只是用一个的列矩阵代替通常的四个分量。
在(1)式中对应于的四个分量有四个方程,由此得到的这些方程中只有三个是独立的。对于满足三个独立方程的一个函数必须适合一定的相容性条件。我们发现,假如满足德布罗意方程(取m=1),那么对于内部坐标的所有值这些方程都满足相容性条件,我们还发现,这个方程是相对论性的,同时粒子的质量必须为正。如果这理论能描述自然界中的任意一个粒子,则这些奇妙的结果会使人们感到惊奇。
人们不能让带电粒子以通常取替换
的方式使粒子与电磁场相互作用.因为这样得到的方程组不再相容,正是由于受到相容性条件这样的限制,所以几乎没有人去从事这种理论研究;同时我没有找到发展这种理论的任何方法,因此没有什么希望使它得到应用。
最近,由苏德森(Sudarshan)和他的同事们进行的研究工作使这种理论取得 了进展。对于a(有四个值》的每一个值有下面的替换
他们扩充了粒子的固有自由度,虽然对每一个r,如同最初描述两个谐振子的一样,然而对不同的r值,反对易,在这些条件下,苏德森证明,方程组是相容的,并且仍然得到一个合理的相对论性理论。
这确实是一个引人注目的结果。它使这个理论更富于灵活性,从而使人们按照(2)式的步骤用通常方式引入与电磁场的相互作用成为可能。虽然,我们对把这种理论用于自然界中的某些粒子将抱有希望,然而还有大盘的研究工作要人们去做。
以这种途径可能得到一个表现出新 特征的新的理论来,这是人们不能由已有理论直接推出的结果。

注:本文曾献给1981年5月新奥尔 莱斯的洛奥拉大学;(Loyola university, New orleans)的狄拉克专题讨论会。
参考文献
[1] Dirac, P. A. M.(1971). Proceedings of the Roy-al Sociely of London Series A, 322,435.
[2] Sudarshan, E. C. G. et. al,(19B2), Proccedings of the Royal Society of LondonSeries A. 379,103.
(陕西师范学院 郭振华译自Interntional Journal of Th-eorfical Physics. Vol,21nos8/9,1982高能物理所郭应焕校)