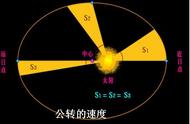
开普勒第二定律的应用非常广泛。比如某行星沿椭圆轨道运行,我们知道它远日点离太阳的距离,又知道近日点离太阳的距离,还知道,还知道过远日点是行星的速率,我们就可以知道过近日点时的行星速率是多少。
开普勒第二定律是对行星运动轨道更准确的描述,为哥白尼的日心说提供了有力证据,并为牛顿后来的万有引力证明提供了论据。不过第二定律只在行星质量比太阳质量小得多的情况下才是精确的。如果考虑到行星也吸引太阳,这便形成了一个二体问题。

二体问题
开普勒第三定律,也称周期定律:各个行星绕太阳公转周期的平方和它们的椭圆轨道的半长轴的立方成正比。论述如下:

后来,经过修正后的第三定律的精确公式为:

牛顿也曾利用开普勒第三定律推导出万有引力定律,牛顿假定太阳质量足够大,不会受到行星运动影响,因此不存在双星系统的问题;太阳和行星均为质点,有质量,无体积,并且太阳和行星的质量分布均满足密度仅与距自身质心距离相关,从而推导出了万有引力定律。
牛顿利用开普勒三大定律推导万有引力定律不是一蹴而就的,他曾在 1665~1666 年间只用离心力定律和开普勒第三定律,因而只能证明圆轨道上的而不是椭圆轨道上的引力平方反比关系。