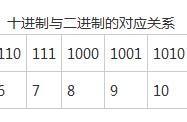
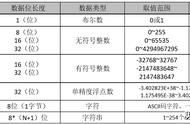
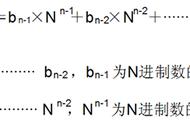按照之前的量化公式,我们就可以得到二进制在 8 位数据上的效率是:
256 ÷ 16 = 16 。
当然,我们不可能一个个进制、位数算过来,估计很多差友都想到了,直接代数化就好了。

假设我们要用 x 进制表达 n 位的数据信息,和之前二进制表达 8 位数据同理:
一共能表达 xn 种不同的信息内容,需要消耗 nx 个表达信息的元件。
x 进制的效率就是 xn / nx

虽然一堆未知数,其实和分数一个道理,分子不变的情况下,分母越小,得数就越大。
所以消耗的资源 ( nx ) 越小,这种进制的效率就越高。
抽奖时分母越少,中奖概率也越高,可我从来只是分母

温馨提示:下方为推导过程,不感兴趣可直接略过看结果。
信息量 I = x^n
消耗的资源P(x)=nx
x进制的效率=x^n/nx
P(x)一定时,x^n最大
[P(x)/n]^n
ln{[P(x)/n]^n}
=[lnP(x)-lnn]n
=nlnP(x)-nlnn
lnP(x)-1-ln(n)=0
n=P(x)/e x=e
前面也提过, e 的值大概是 2.71828 左右,也就是 “ 2.71828 进制 ”是理论上最好的进制。
但是 2.71828 进制是个什么鬼???我数数手指还得掰折 0.28172 根手指?
还是得找个整数,不然工业上可能没法实现了。。。因此和这个数更接近的 “ 三 ”应该是坠吼的!
得到结论:数据表达上效率最高的是三进制,其次是二进制。
三进制... 3 ?似乎联想到了什么