直角易找,一线难求,妙用一线三直角模型速答选择题

一线三直角模型的基本图形是在一条直线上,依次有三个直角,可巧妙构造出一对全等三角形或相似三角形,但实际解题过程中,直角往往容易找到,但那根线却是关键因素,想不到或观察不出来,就构不成相应的模型,解题就此陷入困境。本文取材于一道选择题,实际在解答过程中,不少同学冥思苦想半天仍不得要领,但在指出那根关键的直线后,问题迎刃而解。
题目
如图,在平面直角坐标系中,已知A(0,2),M(m,0)且m>0,分别以AO,AM为边在∠AOM内部作等边△AOB和等边△AMC,连接CB并延长交x轴于点D,则C点的横坐标的值为( )
A.1/2m 3√3/2 B.1/2m √3/2 C.1/2m 2√3/3 D.1/2m √3

解析:
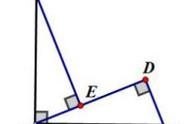
思路的选择应与题目所求吻合,本题需要求点C坐标,于是过点C向x轴作垂线是必须完成的工作之一,但在作完这根辅助线后,许多同学便不知道下一步该何去何从,题目中那两对等边三角形显然是用来构造全等三角形的,先找到它们,即△AOM≌△ABC,于是得到了∠ABC=90°,好,就是它了!如下图:

这个直角顶点为B,它同时也是等边△AOB的一个顶点,过点B再作y轴的垂线,即可得到一线三直角中的那根线了,原来先前过点C作的那根垂线没必要画那么长,如下图:

看吧!经典图例又来了,一线三直角模型,显然可证明图中的△ABE∽△BCF,接下来的工作就极轻松了,简单到口算即可得到结果。
△ABF是含30°角的直角三角形,于是BF=√3,AF=1,由相似三角形的对应边成比例,可得比例式AE:BF=AB:BC,即1:BF=2:m,于是BE=m/2,C点横坐标即可求得1/2m √3.
解题反思:
从刚刚开始的一脸懵,到恍然大悟,恐怕缺少的正是这类模型的积累,因此,每做完一道题,尤其是经过思考的题目,及时归纳总结是提升数学解题能力的最佳方法。一线三直角模型,包括后来的一线三等角,均源于平时的解题积累,只有这些经验刷够了,再面对同类题,便会觉得游刃有余,原来并不难嘛!
,