三点共线与三线共点的证明方法

一、三点共线的常用证明方法
(一)利用平角180°
例1 如图,点D是等腰直角三角形ABC内一点.将△ADC绕点C顺时针旋转90°得到△BEC,点D的对应点为点E.
(1)如果AD:CD:BD=1:2:3,求证:A,D,E三点共线;
(2)如果A,D,E三点共线,AD,CD,BD满足什么样的关系?

解析:(1)连接DE,欲证A、D、E三点共线,只需要证明∠ADE=180°,即证∠ADC ∠CDE=180°.
由旋转,可知:CD=CE,∠DCE=90°,AD=BE,∠ADC=BEC,
所以△CDE是等腰直角三角形,
所以∠CDE=∠CED=45°,
因为AD:CD:BD=1:2:3,
所以可设AD=BE=a,CD=2a,BD=3a,
则DE=2√2a,
所以BE2 DE2=a2 8a2=9a2=BD2,
所以∠BED=90°,
所以∠CEB=135°=∠ADC,
所以∠ADE=135° 45°=180°,
所以A、D、E三点共线;
(2)逆着(1)的思路可知:如果A,D,E三点共线,AD,CD,BD满足的关系是:AD2 2CD2=BD2.
(二)利用平行公理
例2 如图,等边△ABC中,D为AB边上一点(点D不与点A、B重合),连接CD,将CD平移到BE(其中点B和C对应),将△BCD绕着点B逆时针旋转至△BAF,求证:D、F、E三点共线.

解析:连接DE,DF,欲证D、F、E三点共线,只需要证明DE,DF平行于同一条直线即可.
由平移可得:BE平行且等于CD,
所以四边形BCDE是平行四边形,
所以DE//BC;
由旋转,得:BF=BD,∠DBF=∠DBC=60°,
所以△BDF是等边三角形,
所以∠BDF=60°=∠DBC,
所以DF//BC,
由平行公理可知DE、DF是同一条直线,
所以D、F、E三点共线.
二、三线共点的常用证明方法
(一)转化为三点共线的证明
例3 如图,菱形ABCD中,∠B=60°,P是BC延长线上一点,连接AP.点M是线段AP上的点,满足∠AMC=120°,求证:直线AB,CM,PD相交于同一点.

解析:首先设AB、CM相交于点O,连接OD,则欲证直线AB,CM,PD相交于同一点,只需要证明O、D、P三点共线即可.
因为四边形ABCD是菱形,∠B=60°,
所以△ABC和△ACD都是等边三角形,
所以∠CAD=60°,
即∠CAM ∠MAD=60°,
因为∠AMC=120°,
所以∠CAO ∠ACO=60°,
所以∠MAD=∠ACO,
又因为AD//BP,
所以∠MAD=∠APC,
所以∠ACO=∠APC,
又∠OAC=∠ACP=120°,
所以△ACO∽△CPA,
所以AC:CP=AO:AC,
因为AC=CD=AD,
所以CD:CP=AO:AD,
因为∠OAD=∠DCP=60°,
所以△OAD∽△DCP,
所以∠ODA=∠DPC,
所以∠ODP=∠ODA ∠ADC ∠CDP
=∠DPC ∠DCP ∠CDP
=180°,
所以O、D、P三点共线,
所以直线AB,CM,PD相交于同一点O.
(二)利用同一法则
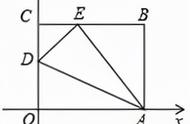
例4 如图,矩形ABCD中,E是BC上的动点,延长EB到F,使BF=BE,G为AD的中点,求证:直线AE,BG,DF三线共点.

解析:设AE、DF相交于点O,连接BO并延长交AD于H,则欲证直线AE,BG,DF三线共点,只需要证明BG和BH是同一条直线,即证点H是AD的中点即可.
因为AD//BC,
所以△OAH∽△OBE,
所以AH:BE=OH:OB,
同理,DH:BF=OH:OB,
所以AH:BE=DH:BF,
因为BE=BF,所以AH=DH,
所以H是AD的中点,
因为G是AD的中点,
所以BH和BG是同一条直线,
所以直线AE,BG,DF三线共点.
,