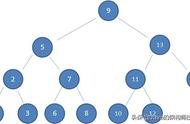
红黑树的删除

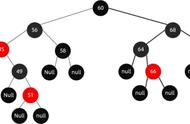
表面是删除172节点,实际上删除节点是172节点的后继,这里找的就是206,也就是y这个节点,那就需要把206(这个是右子树上面的那个最小的点)这个数赋值到z的位置,拷贝到z节点上面去。206被delete后,这个时候206变为237的父节点,如何旋转呢,修复呢?这个时候需要找出206的子树,放到237的位置上的位置上去。
z是被覆盖的节点。
y是真正被delete的点
X是轴心点,以他为轴心
这里的删除也分为2种情况
1. 当要删除的节点,没有左右子树的情况,就只能删除父节点。
2. 第二种,就是上面分析的那点,实际要删除就是右子树上面的最小的那个点。
移除的节点是黑色,才有可能要调整。
为什么删除是4种情况?

//如果移除的节点是黑色的,这个时候需要调整
void rbtree_delete_fixup(rbtree * T,rbtree_node * x)
{
//黑色的点
while((x != T->root) && (x->color == BLACK))
{
//如果是左子树
if(x == x->parrent->left)
{
rbtree_node *w = x->parrent->right;
//如果右子树的颜色是红色
if(w->color == RED)
{
//改变作色
w->color = BLACK;
x->parrent->color = RED;
//左旋
rbtree_left_rotate(T,x->parrent);
w = x->parrent->right;
}
//如果左子树是黑色,右子树是黑色
if((w->left->color == BLACK) && (w->right->color == BLACK))
{
//改变作色
w->color = RED;
//重新制定父节点
x = x->parrent;
}else{
//左子树不是黑色,右子树是黑色
if(w->right->color == BLACK)
{
//改变颜色
w->left->color = BLACK;
w->color = RED;
//并右旋
rbtree_right_rotate(T,w);
w = x->parrent->right;
}
//再左旋
w->color = x->parrent->color;
x->parrent->color = BLACK;
//
w->right->color = BLACK;
rbtree_left_rotate(T,x->parrent);
x = T->root;
}
}else
{
//右子树
rbtree_node *w = x->parrent->left;
if(w->color == RED)
{
w->color = BLACK;
x->parrent->color = RED;
//右旋
rbtree_right_rotate(T,x->parrent);
w = x->parrent->left;
}
//如果左子树是黑色,右子树也是黑色
if((w->left->color == BLACK) && (w->right->color == BLACK))
{
w->color = RED;
x = x->parrent;
}else
{
if(w->left->color == BLACK)
{
w->right->color = BLACK;
w->color = RED;
rbtree_left_rotate(T,w);
w = x->parrent->left;
}
w->color = x->parrent->color;
x->parrent->color = BLACK;
w->left->color = BLACK;
rbtree_right_rotate(T,x->parrent);
x = T->root;
}
}
}
x->color = BLACK;
}
rbtree_node *rbtree_delete(rbtree * T,rbtree_node * z)
{
rbtree_node *y = T->nil;
rbtree_node *x = T->nil;
//如果当前只有一个节点
if((z->left == T->nil) || (z->right == T->nil))
{
y = z;
}else
{
//左右子树都不为空的情况
//寻找节点
y = rbtree_successor(T,z);
}
if(y->left != T->nil)
{
x = y->left;
}else if(y->right != T->nil)
{
x = y->right;
}
x->parrent = y->parrent;
if(y->parrent == T->nil)
{
//如果没有叶子节点
T->root = x;
}else if(y == y->parrent->left)
{
y->parrent->left = x;
}else
{
y->parrent->right = x;
}
if(y != z)
{
z->key = y->key;
z->value = y->value;
}
//调整
if(y->color == BLACK)
{
rbtree_delete_fixup(T,x);
}
/*
//如果这里重复写了,会出现内存段错误
if(y->color == BLACK)
{
rbtree_delete_fixup(T,x);
}
*/
return y;
}
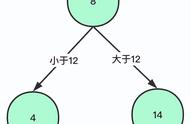
搜索红黑树节点
//搜索节点
rbtree_node *rbtree_search(rbtree *T,KEY_TYPE key)
{
rbtree_node *node = T->root;
while(node != T->nil)
{
if(key < node->key)
{ //小于当前节点,插到左子树
node = node->left;
}else if(key > node->key)
{
//大于当前节点,插到右子树
node = node->right;
}else
{
return node;
}
}
return T->nil;
}
红黑树遍历
//查找红黑树最小值
rbtree_node *rbtree_mini(rbtree *T,rbtree_node *x)
{
while(x->left != T->nil)
{
x = x->left;
}
return x;
}
//查找红黑树最大值
rbtree_node *rbtree_maxi(rbtree *T,rbtree_node *x)
{
while(x->right != T->nil)
{
x = x->right;
}
return x;
}
//中序遍历
void rbtree_traversal(rbtree *T,rbtree_node *node)
{
if(node != T->nil)
{
//递归
rbtree_traversal(T,node->left);
printf("key:%d, color:%d\n", node->key, node->color);
rbtree_traversal(T,node->right);
}
}
//增删改查测试代码
int main()
{
int keyArr[20] = {24,25,13,35,23, 26,67,47,38,98, 20,19,17,49,12, 21,9,18,14,15};
rbtree *T = (rbtree *)malloc(sizeof(rbtree));
if(T == NULL)
{
printf("malloc failed\n");
return -1;
}
T->nil = (rbtree_node*)malloc(sizeof(rbtree_node));
T->nil->color = BLACK;
T->root = T->nil;
rbtree_node *node = T->nil;
int i = 0;
for(i = 0; i < 20; i )
{
node = (rbtree_node*)malloc(sizeof(rbtree_node));
node->key = keyArr[i];
node->value = NULL;
//插入
rbtree_insert(T,node);
}
//中序遍历
rbtree_traversal(T,T->root);
printf("1----------------------------------------\n");
for(i = 0; i < 20; i )
{
//搜索
rbtree_node *node = rbtree_search(T,keyArr[i]);
//删除
rbtree_node *cur = rbtree_delete(T,node);
//释放
free(cur);
//遍历
rbtree_traversal(T,T->root);
printf("2----------------------------------------\n");
}
}
测试:
插入元素,然后中序遍历,并作色

搜索,删除元素,再遍历输出