红黑树和平衡二叉树的优缺点,红黑树为什么是平衡二叉树

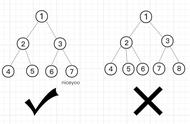
情况2：关注节点是 a，它的叔叔节点 d 是黑色，关注节点 a 是其父节点 b 的右子节点：

1. 关注节点变成节点 a 的父节点 b。
2. 围绕新的关注节点 b 左旋。
3. 跳到情况3。

情况3：如果关注节点是 a，它的叔叔节点 d 是黑色，关注节点 a 是其父节点 b 的左子节点，我们就依次执行下面的操作：

1. 围绕关注节点 a 的祖父节点 c 右旋。
2. 将关注节点 a 的父节点 b、兄弟节点 c 的颜色互换，调整结束。

相比插入，删除就难多了！核心思想是找准关注点，根据关注点跟周围节点排布特征按照一定规则调整。主要俩步骤：

1. 针对删除节点调整后仍要满足节点到叶子节点路径包含相同黑色节点。
2. 针对关注节点二次调整，防止出现2个红色节点。

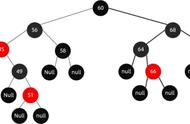
算法导论中说如果删除黑节点X带来黑色平衡破坏，让X的子节点变为黑-黑或红-黑。意思是既然删除了某个黑色节点，那么必然会破坏以这个黑色节点为路径上的黑色平衡，表现为路径中缺少一个黑，所以要想办法补充一个黑色节点(下面会用黑色圆圈表示)。同时如果一个节点既可以红又可以黑，就用红黑两个组成部分表示。

情况1：要删除的节点是 a，它只有一个子节点 b：

1. 删除节点 a，并且把节点 b 替换到节点 a 的位置，这一部分操作跟普通的二叉查找树的删除操作一样。
2. 节点 a 只能是黑色，节点 b 也只能是红色，其他情况均不符合红黑树的定义。此时把节点 b 改为黑色。调整结束，不需要进行二次调整。

情况2：要删除的节点 a 有两个非空子节点，并且它的后继节点就是节点 a 的右子节点 c：

1. 如果节点 a 的后继节点就是右子节点 c，那 c 肯定没有左子树。将c的颜色变为a的颜色，并且用c来覆盖a。
2. 如果节点 c 是黑色，为了不违反红黑树的路径相同原则，给节点 c 的右子节点 d 多加一个黑色圆圈，这个时候节点 d 就成了红 - 黑或者黑 - 黑。
3. 此时关注节点变成了节点 d，第二步的调整操作就会针对关注节点来做。